
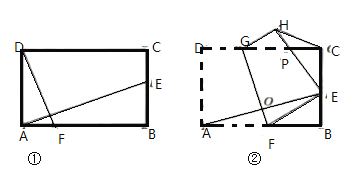
【题目】(1)如图①,在矩形![]() 中,
中,![]() 分别是
分别是![]() 上的点,且
上的点,且![]() ,求
,求![]() 的值;
的值;
(2)如图②,在矩形![]() 中
中![]() (
(![]() 为常数),将矩形
为常数),将矩形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,得到四边形
处,得到四边形![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,连接![]() ,当
,当![]() 时,若
时,若![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)①证明![]() ,利用相似三角形的性质可求出
,利用相似三角形的性质可求出![]() 的值;
的值;
②作![]() 于点
于点![]() ,证明
,证明![]() ,利用相似三角形的性质可求出
,利用相似三角形的性质可求出![]() 的值;
的值;
(2)结论:![]() .如图2中,作GM⊥AB于M.证明:△ABE∽△GMF即可解决问题.
.如图2中,作GM⊥AB于M.证明:△ABE∽△GMF即可解决问题.
(3)先根据余角的性质证明∠BFE=∠CGH,设![]() ,根据勾股定理求出k,再证明△BFE∽△CEP,即可求解.
,根据勾股定理求出k,再证明△BFE∽△CEP,即可求解.
(1)![]() 四边形
四边形![]() 是矩形,
是矩形,
∴![]() ,∠ABC=∠BAD=90°,
,∠ABC=∠BAD=90°,
![]() ,
,
![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)如图②中,作![]() 于点
于点![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
∴![]() ;
;

(3)∵∠CGH+∠GPH=90°,∠CEP+∠CPE=90°,
∴∠CGH=∠CEP,
同理∠BFE=∠CEP,
∴∠BFE=∠CGH,
![]() ,
,
设![]() ,
,
![]() ,
,
![]() .
.
![]() 在
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() 或
或![]() (舍去),
(舍去),
![]() ,BF=4,AB=9,
,BF=4,AB=9,
![]() ,
,
∴BC=6,
∴CE=6-3=3,
∠BFE=∠CEP,∠B=∠PEC,
∴△BFE∽△CEP,
∴![]() ,
,
∴![]() ,
,
∴CP=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】将矩形纸片![]() 沿对角线
沿对角线![]() 翻折,使点
翻折,使点![]() 的对应点
的对应点![]() (落在矩形
(落在矩形![]() 所在平面内,
所在平面内,![]() 与
与![]() 相交于点
相交于点![]() ,接
,接![]() .
.
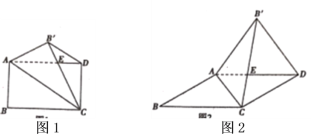
(1)在图1中,
①![]() 和
和![]() 的位置关系为__________________;
的位置关系为__________________;
②将![]() 剪下后展开,得到的图形是_________________;
剪下后展开,得到的图形是_________________;
(2)若图1中的矩形变为平行四边形时(![]() ),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
已知实数m,n满足(2m3+n3+1)(2m3+n3-1)=80,试求2m3+n3的值
解:设2m3+n3=t,则原方程变为(t+1)(t-1)=80,整理得t2-1=80,t2=81, t=±9,所以2m3+n3=±9
上面这种方法称为“换元法”,把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
已知实数x,y满足(4x2+4y2+3)(4x2+4y2-3)=27,求x2+y2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数![]() (k为常数,k ≠0)的图象上,正方形ADEF的面积为16,且BF=2AF,则k值为
(k为常数,k ≠0)的图象上,正方形ADEF的面积为16,且BF=2AF,则k值为
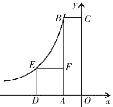
A.-8B.-12C.-24D.-36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7

(1)指出旋转中心和旋转角度.
(2)求DE的长度.
(3)BE与DF垂直吗? 说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日贵州环保行活动“美丽乌江 拒绝污染”正式开启,乌江支流由于长期采磷及磷化工发展造成了总磷污染.当地政府提出五条整改措施,力求在
日贵州环保行活动“美丽乌江 拒绝污染”正式开启,乌江支流由于长期采磷及磷化工发展造成了总磷污染.当地政府提出五条整改措施,力求在![]() 天以内使总磷含量达标(即总磷浓度低于
天以内使总磷含量达标(即总磷浓度低于![]() ).整改过程中,总磷浓度
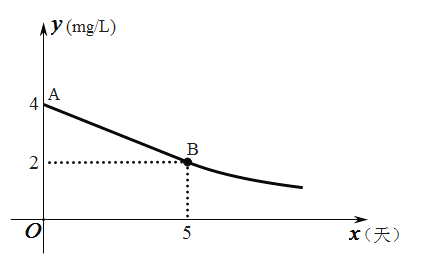
).整改过程中,总磷浓度![]() 与时间
与时间![]() (天)的变化规律如图所示,其中线段
(天)的变化规律如图所示,其中线段![]() 表示前
表示前![]() 天的变化规律,且线段
天的变化规律,且线段![]() 所在直线的表达式为:
所在直线的表达式为:![]() ,从第
,从第![]() 天起,该支流总磷浓度
天起,该支流总磷浓度![]() 与时间
与时间![]() 成反比例关系.
成反比例关系.
(1)求整改全过程中总磷浓度![]() 与时间
与时间![]() 的函数表达式;
的函数表达式;
(2)该支流中总磷的浓度能否在![]() 天以内达标?说明理由.
天以内达标?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax﹣2(a≠0).
(1)该二次函数图象的对称轴是直线 ;
(2)若该二次函数的图象开口向上,当﹣1≤x≤5时,函数图象的最高点为M,最低点为N,点M的纵坐标为![]() ,求点M和点N的坐标;
,求点M和点N的坐标;
(3)若该二次函数的图象开口向下,对于该二次函数图象上的两点A(x1,y1)、B(x2,y2),当x2≥3时,均有y1≥y2,请结合图象,直接写出x1的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与x轴交于点A,B ( A在B的左侧)
与x轴交于点A,B ( A在B的左侧)
(1)如图1,若抛物线的对称轴为直线![]() .
.
①点A的坐标为( , ),点B的坐标为( , );
②求抛物线的函数表达式;
(2)如图2,将(1)中的抛物线向右平移若干个单位,再向下平移若干个单位,使平移后的抛物线经过点O,且与x正半轴交于点C,记平移后的抛物线顶点为P,若![]() 是等腰直角三角形,求点P的坐标.
是等腰直角三角形,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com