
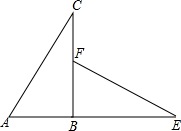
 如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答:
如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答:分析 (1)由条件易得BC和BE,BA和BF为对应边,而△ABC旋转后能与△FBE重合,于是可判断旋转中心为点B;根据旋转的性质得∠ABF等于旋转角,从而得到旋转角度;
(2根据旋转的性质即可判断AC=EF,AC⊥EF.
解答 解:(1)∵BC=BE,BA=BF,
∴BC和BE,BA和BF为对应边,
∵△ABC旋转后能与△FBE重合,
∴旋转中心为点B;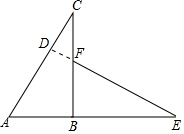
∵∠ABC=90°,
而△ABC旋转后能与△FBE重合,
∴∠ABF等于旋转角,
∴旋转了90度,
故答案为:B,90;
(2)AC⊥EF 理由如下:
延长EF交AC于点D由旋转可知∠C=∠E
∵∠ABC=90°
∴∠C+∠A=90°
∴∠E+∠A=90°
∴∠ADE=90°
∴AC⊥EF.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
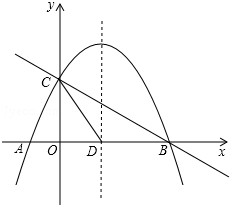 如图,抛物线y=-x2+mx+n与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1,0),C(0,3)
如图,抛物线y=-x2+mx+n与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1,0),C(0,3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
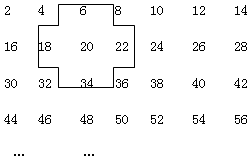 探索规律:将连续的偶数2,4,6,8,…,排成如表:
探索规律:将连续的偶数2,4,6,8,…,排成如表:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com