
·ÖĪö £Ø¢ń£©½«k=1£¬b=1“śČė“śČėµĆ£ŗÅ×ĪļĻߵĽāĪöŹ½ĪŖy=ax2+x+1£¬Ö±ĻߵĽāĪöŹ½ĪŖy=x£¬Č»ŗóĄūÓĆÅä·½·ØĒóµĆÅ×ĪļĻߵĶ„µć×ų±ź£¬Č»ŗó½«Å×ĪļĻßµÄŗįׯ×ų±ź“śČėÖ±ĻߵĽāĪöŹ½ĒóµĆaµÄÖµ¼“æÉ£»
£Ø¢ņ£©£Øi£©Ę½ŅĘŗóÖ±ĻߵĽāĪöŹ½ĪŖy=kx+k2+1£¬ÓÉÖ±ĻßÓėÅ×ĪļĻ߶¼Ö»ÓŠŅ»øö½»µć£¬æÉÖŖ·½³Ģax2+£Øb-k£©x-k2=0ÓŠĮ½øöĻąµČµÄŹµŹżøł£¬¹Ź“Ė”÷=0£¬¼“£Ø4a+1£©k2-2bk+b2=0ŗć³ÉĮ¢£¬¹Ź“Ė4a+1=0ĒŅb=0£¬ÓŚŹĒµĆµ½Å×ĪļĻߵĽāĪöŹ½£»£Øii£©ÉčµćPµÄ×ų±źĪŖ£Øx£¬-$\frac{1}{4}$x2+1£©ŌņµćQµÄ×ų±źĪŖ£Øx£¬2£©£¬D£Øx£¬0£©£¬ŌņPD=|-$\frac{1}{4}$x2+1|£¬OD=|x|£¬QP=$\frac{1}{4}$x2+1£®ŌŚRt”÷OPDÖŠ£¬ŅĄ¾Ż¹“¹É¶ØĄķæÉĒóµĆOP=$\frac{1}{4}$x2+1£¬¹Ź“ĖæɵƵ½OP=PQ£®
½ā“š ½ā£ŗ£Ø¢ń£©½«k=1£¬b=1“śČė“śČėµĆ£ŗÅ×ĪļĻߵĽāĪöŹ½ĪŖy=ax2+x+1£¬Ö±ĻߵĽāĪöŹ½ĪŖy=x£®
”ßy=ax2+x+1=a£Øx+$\frac{1}{2a}$£©2+1-$\frac{1}{4a}$£¬
”ąÅ×ĪļĻߵĶ„µćĪŖ£Ø-$\frac{1}{2a}$£¬1-$\frac{1}{4a}$£©£®
”ßÅ×ĪļĻߵĶ„µćŌŚÖ±Ļßy=xÉĻ£¬
”ą-$\frac{1}{2a}$=1-$\frac{1}{4a}$£¬½āµĆ£ŗa=-$\frac{1}{4}$£®
£Ø¢ņ£©£Øi£©½«Ö±Ļßy=kxĻņÉĻĘ½ŅĘk2+1øöµ„Ī»£¬ĖłµĆÖ±ĻߵĽāĪöŹ½ĪŖy=kx+k2+1£®
”ßĪŽĀŪ·ĒĮ揵ŹżkČ”ŗĪÖµ£¬Ö±ĻßÓėÅ×ĪļĻ߶¼Ö»ÓŠŅ»øö½»µć£¬
”ą·½³Ģkx+k2+1=ax2+bx+1ÓŠĮ½øöĻąµČµÄŹµŹżøł£¬¼“ax2+£Øb-k£©x-k2=0ÓŠĮ½øöĻąµČµÄŹµŹżøł£¬
”ą”÷=£Øb-k£©2+4ak2=£Ø4a+1£©k2-2bk+b2=0£®
”ßĪŽĀŪ·ĒĮ揵ŹżkČ”ŗĪÖµŹ±£¬£Ø4a+1£©k2-2bk+b2=0ŗć³ÉĮ¢£¬
”ą4a+1=0ĒŅb=0£¬
”ąa=-$\frac{1}{4}$£¬b=0£®
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=-$\frac{1}{4}$x2+1£®
£Øii£©Ö¤Ć÷£ŗøł¾ŻĢāŅā£¬»³öĶ¼ĻóČēĶ¼ĖłŹ¾£ŗ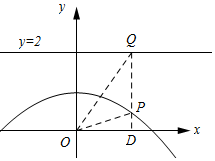
ÉčµćPµÄ×ų±źĪŖ£Øx£¬-$\frac{1}{4}$x2+1£©ŌņµćQµÄ×ų±źĪŖ£Øx£¬2£©£¬D£Øx£¬0£©£®
”ąPD=|-$\frac{1}{4}$x2+1|£¬OD=|x|£¬QP=2-£Ø-$\frac{1}{4}$x2+1£©=$\frac{1}{4}$x2+1£®
ŌŚRt”÷OPDÖŠ£¬ŅĄ¾Ż¹“¹É¶ØĄķµĆ£ŗOP=$\sqrt{{x}^{2}+£Ø-\frac{1}{4}{x}^{2}+1£©^{2}}$=$\sqrt{\frac{1}{16}{x}^{4}+\frac{1}{2}{x}^{2}+1}$=$\frac{1}{4}$x2+1£®
”ąOP=PQ£®
µćĘĄ ±¾ĢāÖ÷ŅŖæ¼²éµÄŹĒ¶ž“ĪŗÆŹżµÄ×ŪŗĻÓ¦ÓĆ£¬½ā“š±¾ĢāÖ÷ŅŖÓ¦ÓĆĮĖÅä·½·ØĒ󶞓ĪŗÆŹżµÄ¶„µć×ų±ź”¢µćµÄ×ų±źÓėŗÆŹż½āĪöŹ½µÄ¹ŲĻµ”¢Ņ»ŌŖ¶ž“Ī·½³ĢøłµÄÅŠ±šŹ½”¢¹“¹É¶ØĄķ£¬ÓÉŹ½×Ó£¬£Ø4a+1£©k2-2bk+b2=0ŗć³ÉĮ¢µĆµ½aŗĶbµÄÖµŹĒ½ā“šĪŹĢā£Ø2£©µÄ¹Ų¼ü£»ĒóµĆPO”¢QPµÄ³¤¶Č£ØÓĆŗ¬xµÄŹ½×Ó±ķŹ¾£©ŹĒ½ā“šĪŹĢā£Ø3£©µÄ¹Ų¼ü£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -1 | B£® | -3 | C£® | 1ŗĶ3 | D£® | -1ŗĶ-3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com