
【题目】我市正大力倡导”垃圾分类“,2015年第一季度某企业按A类垃圾处理费25元/吨、B类垃圾处理费16元/吨的收费标准,共支付垃圾处理费520元.从2015年4月起,收费标准上调为:A类垃圾处理费100元/吨,B类垃圾处理费30元/吨.若该企业2015年第二季度需要处理的A类,B类垃圾的数量与第一季度相同,就要多支付垃圾处理费880元.
(1)该企业第一季度处理的两类垃圾各多少吨?
(2)该企业计划第二季度将上述两种垃圾处理总量减少到24吨,且B类垃圾处理量不超过A类垃圾处理量的3倍,该企业第二季度最少需要支付这两种垃圾处理费共多少元?
【答案】(1)第一季度年处理A类垃圾8吨,B类垃圾20吨;(2)1140元.
【解析】
(1)设该企业第一季度年处理A类垃圾x吨,B类垃圾y吨,根据等量关系:2015年第一季度共支付垃圾处理费520元.和2015年第二季度多支付垃圾处理费880元.列方程组,然后解方程组即可;
(2)设该企业第二季度年处理A类垃圾a吨,B类垃圾b吨,需要支付这两种垃圾处理费共w元,根据条件确定a、b之间的关系以及a的取值范围,求出w与a的函数关系式,利用一次函数的性质可解决问题.
解:(1)设该企业第一季度年处理A类垃圾x吨,B类垃圾y吨,根据题意,得
![]()
解之,得![]()
该企业第一季度年处理A类垃圾8吨,B类垃圾20吨;
(2)设该企业第二季度年处理A类垃圾a吨,B类垃圾b吨,需要支付这两种垃圾处理费共w元,根据题意得,
![]() 解之,得,a≥6,.
解之,得,a≥6,.
![]() .
.
由于w的值随a的增大而增大,所以当a=6时,w取最小值.
最小值为70×6+720=1140(元).
答:该企业第二季度最少需要支付这两种垃圾处理费共1140元.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
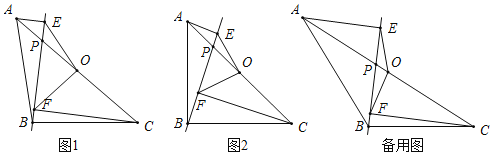
【题目】在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由
(3)若|CF﹣AE|=2,EF=2![]() ,当△POF为等腰三角形时,请直接写出线段OP的长.
,当△POF为等腰三角形时,请直接写出线段OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是( )
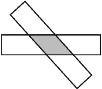
A. 8B. 10C. 10.4D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
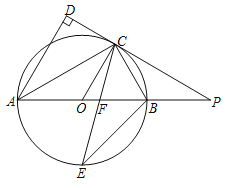
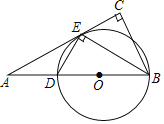
【题目】如图,⊙O是△ABC的外接圆,AC是直径,弦BD=BA,EB⊥DC,交DC的延长线于点E.
(1)求证:BE是⊙O的切线;
(2)当sin∠BCE=![]() ,AB=3时,求AD的长.
,AB=3时,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 是⊙
是⊙![]() 上一点,
上一点, ![]() 与过点
与过点![]() 的切线垂直,垂足为点
的切线垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,弦
,弦![]() 平分∠
平分∠![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证: ![]() 平分∠
平分∠![]() ;
;
(2)求证:PC=PF;
(3)若![]() ,AB=14,求线段
,AB=14,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
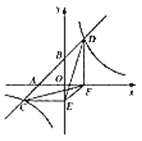
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴,
轴,![]() 轴交于
轴交于![]() ,
,![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,分别过
两点,分别过![]() 、
、![]() 两点作
两点作![]() 轴和
轴和![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,连接
,连接![]() 、
、![]() .下列四个结论:①
.下列四个结论:①![]() 与
与![]() 的面积相等;②
的面积相等;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论是__________.(把你认为正确结论的序号都填上)
.其中正确的结论是__________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】田忌赛马的故事为我们所熟知.小亮与小齐学习概率初步知识后设计了如下游戏:小亮手中有方块l0、8、6三张扑克牌,小齐手中有方块9、7、5三张扑克牌.每人从各自手中取一张牌进行比较,数字大的为本“局”获胜,每次取的牌不能放回.
(1)若每人随机取手中的一张牌进行比赛,求小齐本“局”获胜的概率;
(2)若比赛采用三局两胜制,即胜2局或3局者为本次比赛获胜者.当小亮的三张牌出牌顺序为先出6,再出8,最后出l0时,小齐随机出牌应对,求小齐本次比赛获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,点E、F分别为正方形ABCD的边BC、CD上一点,AC、BD交于点O,且∠EAF=45°,AE,AF分别交对角线BD于点M,N,则有以下结论:①△AOM∽△ADF;②EF=BE+DF;③∠AEB=∠AEF=∠ANM;④S△AEF=2S△AMN,以上结论中,正确的个数有( )个.
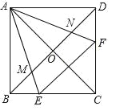
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com