
分析 (1)观光车全部租出每天的净收入=出租自行车的总收入-管理费,根据不等关系:净收入为正,列出不等式求解即可;
(2)由函数解析式是分段函数,在每一段内求出函数最大值,比较得出函数的最大值.
解答 解:(1)由题意知,若观光车能全部租出,则0<x≤100,
由50x-1100>0,
解得x>22,
又∵x是5的倍数,
∴每辆车的日租金至少应为25元;
(2)设每天的净收入为y元,
当0<x≤100时,y1=50x-1100,
∵y1随x的增大而增大,
∴当x=100时,y1的最大值为50×100-1100=3900;
当x>100时,
y2=(50-$\frac{x-100}{5}$)x-1100
=50x-$\frac{1}{5}$x2+20x-1100
=-$\frac{1}{5}$x2+70x-1100
=-$\frac{1}{5}$(x-175)2+5025,
当x=175时,y2的最大值为5025,
5025>3900,
故当每辆车的日租金为175元时,每天的净收入最多是5025元.
点评 本题用分段函数模型考查了一次函数,二次函数的性质与应用,解决问题的关键是弄清题意,分清收费方式.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:选择题
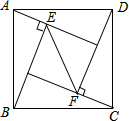 如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )| A. | 7 | B. | 8 | C. | 7$\sqrt{2}$ | D. | 7$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )
如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m+n | B. | n-m | C. | m-n | D. | -m-n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四个角相等的四边形是矩形 | |
| B. | 四边相等的四边形是正方形 | |
| C. | 对角线相等的四边形是菱形 | |
| D. | 对角线互相垂直的四边形是平行四边形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com