

 与⊙P相切;(3)1.5或6
与⊙P相切;(3)1.5或6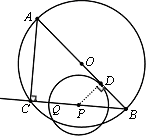
 .∵P为BC的中点,∴PB=6cm.
.∵P为BC的中点,∴PB=6cm. ,∴PD ="3.6(cm)" .
,∴PD ="3.6(cm)" .  与⊙P相切.
与⊙P相切.  时,
时, (cm)
(cm)  ,即圆心
,即圆心 到直线
到直线 的距离等于⊙P的半径.
的距离等于⊙P的半径.  与⊙P相切.
与⊙P相切.  .
.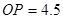 . ∵点P在⊙O内部,∴⊙P与⊙O只能内切.
. ∵点P在⊙O内部,∴⊙P与⊙O只能内切.  或
或 ,∴ =1.5或6.
,∴ =1.5或6. 

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:单选题

A. | B.1 |
C. 或1 或1 | D. 或1或 或1或 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,点P在边AB上,且BP=3AP,如果圆P是以点P为圆心,PD为半径的圆,那么下列判断正确的是
,点P在边AB上,且BP=3AP,如果圆P是以点P为圆心,PD为半径的圆,那么下列判断正确的是查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ),点O是这段弧的圆心,C是
),点O是这段弧的圆心,C是 上一点,OC⊥AB,垂足为D,AB=300m,CD=50m,则这段弯路的半径是 m.
上一点,OC⊥AB,垂足为D,AB=300m,CD=50m,则这段弯路的半径是 m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com