练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在△ABC中，AB=10，AC=2 ，BC边上的高AD=6，则另一边BC等于（ ）
    A.10
    B.8
    C.6或10
    D.8或10

    【答案】C
    【解析】解：根据题意画出图形，如图所示，
    如图1所示，AB=10，AC=2 ，AD=6，
    在Rt△ABD和Rt△ACD中，
    根据勾股定理得：BD= =8，CD= =2，
    此时BC=BD+CD=8+2=10；
    如图2所示，AB=10，AC=2 ，AD=6，
    在Rt△ABD和Rt△ACD中，
    根据勾股定理得：BD= =8，CD= =2，此时BC=BD﹣CD=8﹣2=6，
    则BC的长为6或10．
    故选C．

    此题考查了勾股定理，熟练掌握勾股定理是解本题的关键．分两种情况考虑，如图所示，分别在直角三角形ABC与直角三角形ACD中，利用勾股定理求出BD与CD的长，即可求出BC的长．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．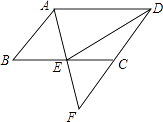

    （1）求证：AB=CF；
    （2）连接DE，若AD=2AB，求证：DE⊥AF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人利用扑克牌玩“10点”游戏，游戏规则如下：
    ①将牌面数字作为“点数”，如红桃6的“点数”就是6（牌面点数与牌的花色无关）；
    ②两人摸牌结束时，将所摸牌的“点数”相加，若“点数”之和小于或等于10，此时“点数”之和就是“最终点数”；若“点数”之和大于10，则“最终点数”是0；
    ③游戏结束前双方均不知道对方“点数”；
    ④判定游戏结果的依据是：“最终点数”大的一方获胜，“最终点数”相等时不分胜负．
    现甲、乙均各自摸了两张牌，数字之和都是5，这时桌上还有四张背面朝上的扑克牌，牌面数字分别是4，5，6，7．

    （1）若甲从桌上继续摸一张扑克牌，乙不再摸牌，则甲获胜的概率为；
    （2）若甲先从桌上继续摸一张扑克牌，接着乙从剩下的扑克牌中摸出一张牌，然后双方不再摸牌．请用树状图或表格表示出这次摸牌后所有可能的结果，再列表呈现甲、乙的“最终点数”，并求乙获胜的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB=6，O是AB的中点，直线l经过点O，∠1=120°，P是直线l上一点，当△APB为直角三角形时，AP= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°AO是△ABC的角平分线．以O为圆心，OC为半径作⊙O．

    （1）求证：AB是⊙O的切线．
    （2）已知AO角⊙O于点E，延长AO交⊙O于点D，tanD= ，求 的值．
    （3）在（2）的条件下，设⊙O的半径为3，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】
    （1）计算：（ ）﹣1+（π﹣3.14）0﹣2sin60°﹣ +|1﹣3 |；
    （2）先化简，再求值：
    （a+1﹣ ）÷（ ），其中a=2+ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】大明因急事在运行中的自动扶梯上行走去二楼（如图1），图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时，距自动扶梯起点的距离与时间之间的关系．下面四个图中，虚线OC能大致表示大明在停止运行（即静止）的自动扶梯上行走去二楼时，距自动扶梯起点的距离与时间关系的是（　　）

    A.
    B.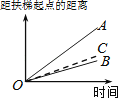
    C.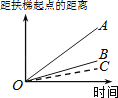
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线AB和抛物线交于点A（﹣4，0），B（0，4），且点B是抛物线的顶点．

    （1）求直线AB和抛物线的解析式．
    （2）点P是直线上方抛物线上的一点，求当△PAB面积最大时点P的坐标．
    （3）M是直线AB上一动点，在平面直角坐标系内是否存在点N，使以O、B、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，矩形ABOC的两边在坐标轴上，OB=1，点A在函数y=﹣ （x＜0）的图象上，将此矩形向右平移3个单位长度到A1B1O1C1的位置，此时点A1在函数y= （x＞0）的图象上，C1O1与此图象交于点P，则点P的纵坐标是（　　）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案