
【题目】某校分别于2015年、2016年春季随机调查相同数量的学生,对学生做家务的情况进行调查(开展情况分为“基本不做”、“有时做”、“常常做”、“每天做”四种),绘制成部分统计图如下.
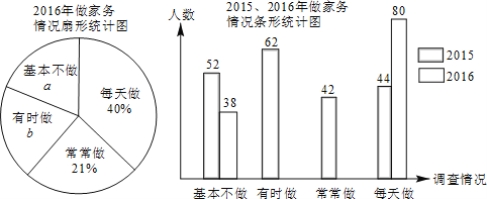
请根据图中信息,解答下列问题:
(1)a=______%,b=______%,“每天做”对应阴影的圆心角为______°;
(2)请你补全条形统计图;
(3)若该校2016年共有1200名学生,请你估计其中“每天做”家务的学生有多少名?
【答案】(1)19,20,144;(2)见解析;(3)480
【解析】
(1)根据统计图可以求得而2016年抽调的学生数,从而可以求得a、b的值以及“每天做”对应的圆心角的度数;
(2)根据统计图可以求得“有时做”、“常常做”的人数,从而可以将条形统计图补充完整;
(3)根据统计图可以估计“每天做”家务的学生的人数.
解:(1)由题意可得,
2016年抽调的学生数为:80÷40%=200,
则a=38÷200×100%=19%,
∴b=1-19%-21%-40%=20%,
“每天做”对应的圆心角为:360°×40%=144°,
故答案为:19,20,144;
(2)“有时做”的人数为:20%×200=40,
“常常做”的人数为:200×21%=42,
补全的条形统计图如下图所示,
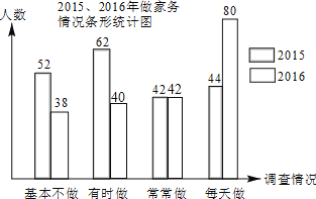
(3)由题意可得,
“每天做”家务的学生有:1200×40%=480(人),
即该校每天做家务的学生有480人.


科目:初中数学 来源: 题型:
【题目】为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查.已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如图所示的统计图表.
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
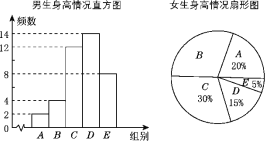
根据图表中提供的信息,回答下列问题:
(1)在样本中,男生身高的中位数落在________组(填组别序号),女生身高在B组的人数有________人;
(2)在样本中,身高在150≤x<155之间的人数共有________人,身高人数最多的在________组(填组别序号);
(3)已知该校共有男生500人、女生480人,请估计身高在155≤x<165之间的学生有多少人
查看答案和解析>>
科目:初中数学 来源: 题型:
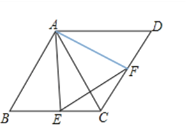
【题目】菱形ABCD中,∠B=60°,点E,F分别是BC,CD上的两个动点,且始终保持∠AEF=60°.
(1)试判断△AEF的形状并说明理由;
(2)若菱形的边长为2,求△ECF周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数![]() (a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为
(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为![]() ,直线l的解析式为y=x.
,直线l的解析式为y=x.
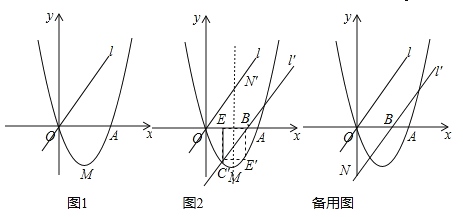
(1)求二次函数的解析式;
(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;
(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E为AB的中点,F为BC上任意一点,把△BEF沿直线EF翻折,点B的对应点B′落在对角线AC上,则与∠FEB一定相等的角(不含∠FEB)有( )
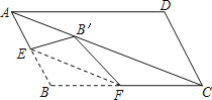
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数的解析式为![]() .
.
(1)它与![]() 轴的交点的坐标为________,顶点坐标为________;
轴的交点的坐标为________,顶点坐标为________;
(2)在给定的坐标系中画出这个二次函数的图象,并求出抛物线与坐标轴的交点所组成的三角形的面积;
(3)根据图象直接写出抛物线在![]() 范围内,函数值
范围内,函数值![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在点B处,直角顶点F在CD的延长线上,BF与AD交于点G,斜边与CD交于点E![]() ,若CE=1,则DG的长为( )
,若CE=1,则DG的长为( )
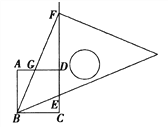
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
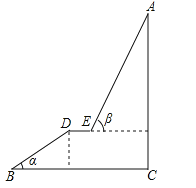
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出的以下四个结论:①AE=CF; ②△EPF一定是等腰直角三角形; ③S四边形AEPF=![]() S△ABC;④当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP。(点E不与A、B重合),上述结论中始终正确的有_____.(写序号)
S△ABC;④当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP。(点E不与A、B重合),上述结论中始终正确的有_____.(写序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com