
【题目】问题引入:
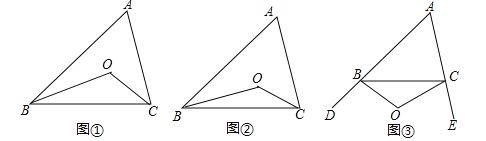
(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);如图②,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示)
∠ACB,∠A=α,则∠BOC= (用α表示)
拓展研究:
(2)如图③,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= (用α表示),并说明理由.
∠ECB,∠A=α,请猜想∠BOC= (用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .

【答案】(1)90°+![]() α,120°+
α,120°+![]() α;(2)120°-
α;(2)120°-![]() α;(3)
α;(3)![]() .
.
【解析】
试题分析:(1)如图①,∵∠ABC与∠ACB的平分线相交于点O,∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∴∠OBC+∠OCB=
∠ACB,∴∠OBC+∠OCB=![]() (∠ABC+∠ACB),在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)
(∠ABC+∠ACB),在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣![]() (∠ABC+∠ACB)=180°﹣
(∠ABC+∠ACB)=180°﹣![]() (180°﹣∠A)=90°+
(180°﹣∠A)=90°+![]() ∠A=90°+
∠A=90°+![]() α;
α;
如图②,在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣![]() (∠ABC+∠ACB)=180°﹣
(∠ABC+∠ACB)=180°﹣![]() (180°﹣∠A)=120°+
(180°﹣∠A)=120°+![]() ∠A=120°+
∠A=120°+![]() α;
α;
(2)如图③,在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣![]() (∠DBC+∠ECB)=180°﹣
(∠DBC+∠ECB)=180°﹣![]() (∠A+∠ACB+∠A+ABC)=180°﹣
(∠A+∠ACB+∠A+ABC)=180°﹣![]() (∠A+180°)=120°﹣
(∠A+180°)=120°﹣![]() α;
α;
(3)在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣![]() (∠DBC+∠ECB)=180°﹣
(∠DBC+∠ECB)=180°﹣![]() (∠A+∠ACB+∠A+ABC)=180°﹣
(∠A+∠ACB+∠A+ABC)=180°﹣![]() (∠A+180°)
(∠A+180°)
=![]() .
.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】老师给出一个二次函数,甲、乙两名同学各指出这个函数的一个性质.甲:函数图象的顶点在x轴上;乙:抛物线开口向下;已知这两位同学的描述都正确,请你写出满足上述所有性质的一个二次函数表达式_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.哥哥的身高比弟弟高是必然事件
B.今年中秋节有雨是不确定事件
C.随机抛一枚均匀的硬币两次,都是正面朝上是不可能事件
D.“彩票中奖的概率为 ![]() ”表示买5张彩票肯定会中奖
”表示买5张彩票肯定会中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
在一个三角形中,各边和它所对角的正弦的比相等,![]() ,利用上述结论可以求解如下题目:
,利用上述结论可以求解如下题目:
在△ABC中,∠A、∠B、∠C的对边分别为a,b,c.若∠A=45°,∠B=30°,a=6,求b.
解:在△ABC中,∵![]() ,∴
,∴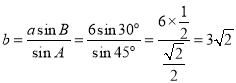 .
.
理解应用:
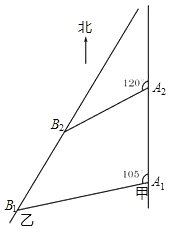
如图,甲船以每小时![]() 海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距
海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距![]() 海里.
海里.
(1)判断△A1A2B2的形状,并给出证明;
(2)求乙船每小时航行多少海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系是 ,位置关系是 ;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com