
【题目】对于自变量x的不同的取值范围,有着不同的对应关系,这样的函数通常叫做分段函数.它是一个函数,而不是几个函数. 分段函数在自变量x的不同的取值范围内,函数的表达式也不同.例如:![]() 是分段函数.
是分段函数.
当![]() 时,它是二次函数
时,它是二次函数![]() ;当
;当![]() 时,它是正比例函数
时,它是正比例函数![]() .
.
(1)请在平面直角坐标系中画出函数![]() 的图象;
的图象;
(2)求出y轴左侧图象的最低点的坐标;
(3)当![]() 时,求自变量x的值.
时,求自变量x的值.
 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作已知角的角平分线.
已知:如图,∠BAC.求作:∠BAC的角平分线AP.
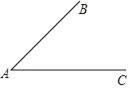
小霞的作法如下:
(1)如图,在平面内任取一点O;
(2)以点O为圆心,AO为半径作圆,交射线AB于点D,交射线AC于点E;
(3)连接DE,过点O作射线OP垂直于线段DE,交⊙O于点P;
(4)过点P作射线AP.
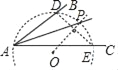
所以射线AP为所求.
老师说:“小霞的作法正确.”
请回答:小霞的作图依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
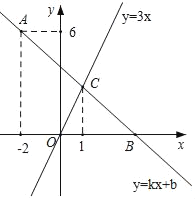
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)请直接写出不等式kx+b﹣3x>0的解集.
(3)若点D在y轴上,且满足S△BCD=2S△BOC,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州某游乐园门票价格为每人100元,20人以上(含20人)的团体票8折优惠.
(1)建兰中学初二年级一等奖学金获得者共有18人,学校奖励他们去游玩,你认为学校买18张门票,还是多买2张(买20张)购团体票更合算?
(2)如果获奖的学生不足20人,那么人数达到多少人时购买团体票比买普通票更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形![]() (三角形的三个顶点都在小正方形的顶点上)
(三角形的三个顶点都在小正方形的顶点上)
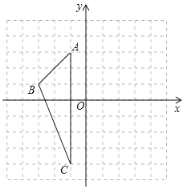
(1)写出![]() 的面积;
的面积;
(2)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)写出点![]() 及其对称点
及其对称点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.
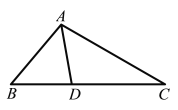
(1)如图,在△ABC中,AD为角平分线,∠B=50°,∠C=30°,求证:AD为△ABC的优美线;
(2)在△ABC中,∠B=46°,AD是△ABC的优美线,且△ABD是以AB为腰的等腰三角形,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,已知AB>BC.
(1)实践与操作:作∠ADC的平分线交AB于点E,在DC上截取DF=AD,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形AEFD的形状,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
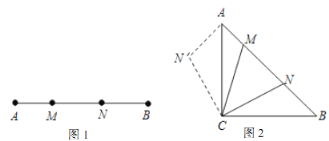
【题目】定义:如(图1),点![]() 把线段
把线段![]() 分割成
分割成![]() 和
和![]() ,若以
,若以![]() 为边的三角形是一个直角三角形,则称点
为边的三角形是一个直角三角形,则称点![]() 是线段
是线段![]() 的勾股分割点.
的勾股分割点.
(1)已知点![]() 是线段
是线段![]() 的勾股分割点,若
的勾股分割点,若![]() ,求
,求![]() 的长;
的长;
(2)如(图2),在等腰直角![]() 中,
中, ![]() ,点
,点![]() 为边
为边![]() 上两点,满足
上两点,满足![]() ,求证:点
,求证:点![]() 是线段
是线段![]() 的勾股分割点;阳阳同学在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把
的勾股分割点;阳阳同学在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 试一试.请根据陈老师的提示完成第(2)小题的证明过程.
试一试.请根据陈老师的提示完成第(2)小题的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )

A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com