练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
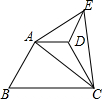
    10．如图，将梯形ABCD沿直线AC翻折，点B落在点E处，联结ED，如果∠B=60°，∠ACB=40°，ED∥AB，那么∠AED的度数为20°．

    分析 根据平行线的性质得到∠BAD=180°-∠B=120°，∠ADE=∠BAD=120°，由三角形内角和定理可求∠BAC，由折叠的性质得∠EAB的度数，再根据角的和差关系可求∠DAE的度数，再由三角形内角和定理可求∠AED的度数．

    解答 解：∵AD∥BC，
    ∴∠BAD=180°-∠B=120°，
    ∵ED∥AB，
    ∴∠ADE=∠BAD=120°，
    ∵∠B=60°，∠ACB=40°，
    ∴∠BAC=80°，
    由折叠的性质得∠EAB=2∠BAC=160°，
    ∴∠DAE=160°-120°=40°，
    ∴∠AED=180°-40°-120°=20°．
    故答案为：20°．

    点评 本题考查了翻折变换（折叠问题），平行线的性质，三角形内角和定理，正确的识别图形是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    20．我们规定：将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“等积线”，等积线被这个平面图形截得的线段叫做该图形的“等积线段”（例如三角形的中线就是三角形的等积线段）．已知菱形的边长为4，且有一个内角为60°，设它的等积线段长为m，则m的取值范围是2$\sqrt{3}$≤m≤4$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

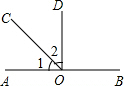    1．如图，点O在直线AB上，∠1=$\frac{1}{3}$∠BOC，OC是∠AOD的平分线；
    （1）求：∠2的度数；
    （2）试说明：OD⊥AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．方程组$\left\{\begin{array}{l}{2x+y=□}\\{x+y=3}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=□}\end{array}\right.$，则被遮盖的两个数分别为（　　）
    A．2，1B．2，3C．5，1D．2，4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图，在边长为1的菱形ABCD中，∠DAB=60°，连接对角线AC，以AC为边作第二个ACC1D1，使∠D1AC=60°；连接AC1，再以AC1为边作第三个菱形AC1C2D2，使∠D2AC1=60°；…，按此规律所作的第2017个菱形的边长为（　　）
    A．（$\frac{\sqrt{3}}{2}$）2016B．（$\sqrt{3}$）2016C．22017D．（$\sqrt{3}$）2017

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，某学生在旗杆EF与实验楼CD之间的A处，测得∠EAF=60°，然后向左移动10米到B处，测得∠EBF=30°，∠CBD=45°，tan∠CAD=$\frac{3}{4}$．
    （1）求旗杆EF的高（结果保留根号）；
    （2）求旗杆EF与实验楼CD之间的水平距离DF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列运算正确的是（　　）
    A．$\sqrt{4}$=±2B．（-3）3=27C．$\sqrt{16}$=4D．$\root{3}{9}$=3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，小明于堤边A处垂钓，河堤AB的坡比为1：$\sqrt{3}$，坡长为3米，钓竿AC的倾斜角是60°，其长为6米，若钓竿AC与钓鱼线CD的夹角为60°，求浮漂D与河堤下端B之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，在等边△ABC中，点D为边BC的中点，以AD为边作等边△ADE，连接BE．
    求证：BE=BD．

    查看答案和解析>>

    同步练习册答案