
���� ��1��������ȡ����ʽ���Ե�ʽ����߽�����ʽ�ֽ⣬����ת��Ϊ����ʽ֮��Ϊ0����ʽ��
��2����ԭ������ת��Ϊ����һԪ���η����飬Ȼ��ⷽ���鼴�ɣ�
��3�����������г�����x�IJ���ʽ�飬ͨ���ⲻ��ʽ��������x��ȡֵ��Χ��
��� �⣺��1����ԭ���̣���
x��x-3��=0��
��������һ�η��̵ã�x=0��x=3��
����ԭ���̵Ľ�Ϊ��x=0��x=3��
��2����ԭ������õ�������$\left\{\begin{array}{l}x+3y=0\\ x+y=4\end{array}\right.$�� $\left\{\begin{array}{l}x-3y=0\\ x+y=4\end{array}\right.$��
�⣨��$\left\{\begin{array}{l}x=6\\ y=-2\end{array}\right.$��
�⣨��$\left\{\begin{array}{l}x=3\\ y=1\end{array}\right.$��
��ԭ������Ľ�Ϊ$\left\{\begin{array}{l}x=6\\ y=-2\end{array}\right.$��$\left\{\begin{array}{l}x=3\\ y=1\end{array}\right.$��
��3��ԭ����ʽ�ɻ�Ϊ��
��$\left\{\begin{array}{l}x-3��0\\ x+1��0\end{array}\right.$�� ��$\left\{\begin{array}{l}x-3��0\\ x+1��0\end{array}\right.$
�ⲻ������⣬
�ⲻ��ʽ�ڿɵ�-1��x��3��
����ԭ����ʽ�Ľ⼯Ϊ-1��x��3��
���� ���⿼����һԪһ�β���ʽ���Ӧ�ã������ǽ����x��һԪ���η��̣����ǽ����x�Ķ�Ԫ���η����飬�����Ƚ��ݣ�Ȼ��ⷽ�̣������飩��


 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
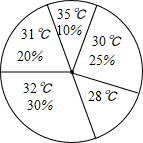 ij������ͳ����60�����������£�����������ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��֪��60����������µ�ƽ��ֵΪ31�森
ij������ͳ����60�����������£�����������ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��֪��60����������µ�ƽ��ֵΪ31�森�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ���� | C�� | ���� | D�� | �ཻ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
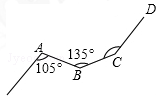 ��ͼ��һ����·��һ�����ӱ�ʱ��������Ƶ������������һ�ιյĽ�A��105�㣬�ڶ��ŹյĽ�B��135�㣬�����ιյĽ��ǡ�C����ʱ�ĵ�·ǡ�ú͵�һ�ι���֮ǰ�ĵ�·ƽ�У���ô��C�Ķ���Ϊ��������
��ͼ��һ����·��һ�����ӱ�ʱ��������Ƶ������������һ�ιյĽ�A��105�㣬�ڶ��ŹյĽ�B��135�㣬�����ιյĽ��ǡ�C����ʱ�ĵ�·ǡ�ú͵�һ�ι���֮ǰ�ĵ�·ƽ�У���ô��C�Ķ���Ϊ��������| A�� | 130�� | B�� | 135�� | C�� | 140�� | D�� | 150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
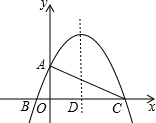 ��ͼ����֪���κ���y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��ͼ����y�ύ�ڵ�A����x�ύ��B��C���㣬��Գ�����x�ύ�ڵ�D������AC��
��ͼ����֪���κ���y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��ͼ����y�ύ�ڵ�A����x�ύ��B��C���㣬��Գ�����x�ύ�ڵ�D������AC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 6 | C�� | 5 | D�� | 3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com