
分析 先化简题目中的式子,然后将使得原分式有意义的x的值代入求值即可解答本题.
解答 解:(x-7+$\frac{25}{x+3}$)÷$\frac{x-2}{{x}^{2}-9}$
=$\frac{(x-7)(x+3)+25}{x+3}×\frac{(x+3)(x-3)}{x-2}$
=$\frac{{x}^{2}-4x+4}{x+3}×\frac{(x+3)(x-3)}{x-2}$
=$\frac{(x-2)^{2}}{x+3}×\frac{(x+3)(x-3)}{x-2}$
=(x-2)(x-3)
=x2-5x+6,
当x=-2时,原式=(-2)2-5×(-2)+6=20.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法,注意所取得x的值必须使得原分式有意义.


科目:初中数学 来源: 题型:解答题
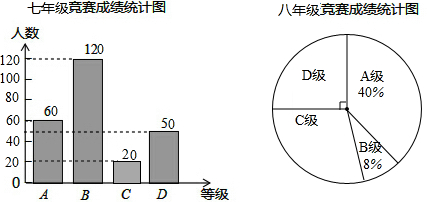
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,C是AD的中点,⊙O的切线BD交AC的延长线于点D,E是OB上一点,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
如图,AB是⊙O的直径,C是AD的中点,⊙O的切线BD交AC的延长线于点D,E是OB上一点,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
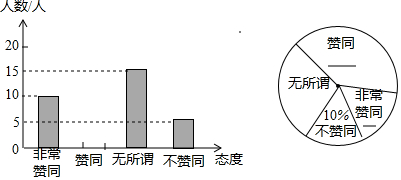
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
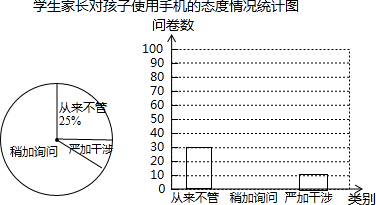
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com