
【题目】我们可用![]() 表示以
表示以![]() 为自变量的函数,如一次函数
为自变量的函数,如一次函数![]() ,可表示为
,可表示为![]() ,且
,且![]() ,
,![]() ,定义:若存在实数
,定义:若存在实数![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点,例如:
的不动点,例如:![]() ,令
,令![]() ,得
,得![]() ,那么
,那么![]() 的不动点是1.
的不动点是1.
(1)已知函数![]() ,求
,求![]() 的不动点.
的不动点.
(2)函数![]() (
(![]() 是常数)的图象上存在不动点吗?若存在,请求出不动点;若不存在,请说明理由;
是常数)的图象上存在不动点吗?若存在,请求出不动点;若不存在,请说明理由;
(3)已知函数![]() (
(![]() ),当
),当![]() 时,若一次函数
时,若一次函数![]() 与二次函数
与二次函数![]() 的交点为
的交点为![]() ,即
,即![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且
的不动点,且![]() 两点关于直线
两点关于直线![]() 对称,求
对称,求![]() 的取值范围.
的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
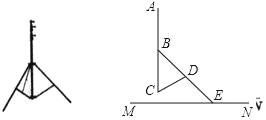
【题目】某数码产品专卖店的一块摄像机支架如图所示,将该支架打开立于地面MN上,主杆AC与地面垂直,调节支架使得脚架BE与主杆AC的夹角∠CBE=45°,这时支架CD与主杆AC的夹角∠BCD恰好等于60°,若主杆最高点A到调节旋钮B的距离为40cm.支架CD的长度为30cm,旋转钮D是脚架BE的中点,求脚架BE的长度和支架最高点A到地面的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场采购员要到厂家批发购买篮球和排球共![]() 个,篮球个数不少于排球个数,付款总额不得超过
个,篮球个数不少于排球个数,付款总额不得超过![]() 元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购
元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购![]() 个篮球.
个篮球.
品名 | 厂家批发价/元/个 | 商场零售价/元/个 |
篮球 |
|
|
排球 |
|
|
(1)求该商场采购费用![]() (单位:元)与
(单位:元)与![]() (单位:个)的函数关系式,并写出自变最
(单位:个)的函数关系式,并写出自变最![]() 的取值范围:
的取值范围:
(2)该商场把这![]() 个球全都以零售价售出,求商场能获得的最大利润;
个球全都以零售价售出,求商场能获得的最大利润;
(3)受原材料和工艺调整等因素影响,采购员实际采购时,低球的批发价上调了![]() 元/个,同时排球批发价下调了
元/个,同时排球批发价下调了![]() 元/个.该体有用品商场决定不调整商场零售价,发现将
元/个.该体有用品商场决定不调整商场零售价,发现将![]() 个球全部卖出获得的最低利润是
个球全部卖出获得的最低利润是![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样大小的黑色棋子按如图所示的规律摆放:

(1)分别写出第6、7两个图形各有多少颗黑色棋子?
(2)写出第n个图形黑色棋子的颗数?
(3)是否存在某个图形有1020颗黑色棋子?若存在,求出是第几个图形;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点 P(-2,4)关于 y 轴的对称点 P'在反比例函数 y=![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求此反比例函数关系式;
(2)当 x 在什么范围取值时,y 是小于 1 的正数?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com