
【题目】![]() 如图
如图![]() ,在
,在![]() 中,
中,![]() ,若
,若![]() 是
是![]() 和
和![]() 的平分线交点,求
的平分线交点,求![]() 的度数。
的度数。

![]() 若是内任意一点,试探究
若是内任意一点,试探究![]() 与
与![]() 之间的关系,并说明理由
之间的关系,并说明理由

![]() 请你直接利用以上结论,解决以下问题:
请你直接利用以上结论,解决以下问题:
①图![]() 中点
中点![]() 为
为![]() 内任意一点,若
内任意一点,若![]() 则
则![]()
![]()

②如图![]() 平分
平分![]() 平分
平分![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)∠BDC=125°;(2)∠BDC=∠BAC+∠ABD+∠ACD,理由见解析;(3)①60;②∠DCE=90°.
【解析】
(1)根据三角形的内角和与DB平分∠ABC,DC平分∠ACB可求得∠DBC+∠DCB的度数,再在△DBC中应用三角形内角和定理即可求出结果;
(2)作射线AD,再运用三角形的外角性质即可得出结论;
(3)①直接应用(2)的结论计算即可;
②先由(2)的结论求出∠ADB+∠AEB的度数,再由CD平分∠ADB,CE平分∠ACB可求出∠ADC+∠AEC的度数,然后再运用(2)的结论即可求出结果.
解:(1)∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=180°-70°=110°,
∵DB平分∠ABC,DC平分∠ACB,
∴∠DBC=![]() ∠ABC,∠DCB=
∠ABC,∠DCB=![]() ∠ACB,
∠ACB,
∴∠DBC+∠DCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×110°=55°,
×110°=55°,
∴∠BDC=180°-55°=125°;
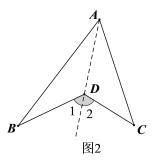
(2)∠BDC=∠BAC+∠ABD+∠ACD,理由如下:
如图2,作射线AD,∵∠1、∠2分别是△ABD和△ACD的外角,
∴∠1=∠BAD+∠ABD,∠2=∠CAD+∠ACD,
∴∠BDC=∠1+∠2=∠BAD+∠ABD+∠CAD+∠ACD=∠BAC+∠ABD+∠ACD.
(3)①由(2)的结论可得:∠ABD+∠ACD=∠BDC―∠A=110°-50°=60°;故答案为60;
②由(2)的结论可得:∠ADB+∠AEB=∠DBE―∠A=130°-50°=80°;
∵CD平分∠ADB,CE平分∠ACB,
∴∠ADC=![]() ∠ADB,∠AEC=
∠ADB,∠AEC=![]() ∠AEB,
∠AEB,
∴∠ADC+∠AEC=![]() (∠ADB+∠AEB)=
(∠ADB+∠AEB)=![]() ×80°=40°,
×80°=40°,
又∵∠DCE=∠ADC+∠A+∠AEC,
∴∠DCE=50°+40°=90°.


科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.

(1)写出商场销售这种工具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各式,能简算的要简算
(1)﹣32﹣(﹣5)3×(![]() )2﹣15÷|﹣3|
)2﹣15÷|﹣3|
(2)(﹣3)×![]() +8×(﹣2
+8×(﹣2![]() )﹣11÷(﹣
)﹣11÷(﹣![]() )
)
(3)﹣4﹣2×32+(﹣2×32)
(4)(﹣48)÷(﹣2)3﹣(﹣25)×(﹣4)+(﹣2)2
查看答案和解析>>
科目:初中数学 来源: 题型:
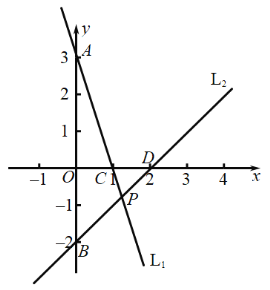
【题目】如图,L1、L2分别表示两个一次函数的图象,它们相交于点P.
(1)求出两条直线的函数关系式;
(2)点P的坐标可看作是哪个二元一次方程组的解?
(3)求出图中△APB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形按一定规律排列,观察并回答:

(1)依照此规律,第四个图形共有 个★,第六个图形共有 个★;
(2)第n个图形中有★ 个;
(3)根据(2)中的结论,第几个图形中有2020个★?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应括号里:
![]() ,8.2,-7,0,-0.3,102 ,-2.1010010001…,
,8.2,-7,0,-0.3,102 ,-2.1010010001…,![]() ,
,![]()
非负整数集合:{ …}
分数集合:{ …}
无理数集合:{ …}
负数集合:{ …}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,若取前3格子中的任意两个数记作![]() ,且
,且![]() ,那么所有的
,那么所有的![]() 的和可以通过计算
的和可以通过计算![]() 得到,其结果为_____,若
得到,其结果为_____,若![]() 为前
为前![]() 格子中的任意两个数,且
格子中的任意两个数,且![]() ,则所有的
,则所有的![]() 的和为_____.
的和为_____.
9 | ★ | ☆ | x | ﹣6 | 2 | …… |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x+bx+c的顶点为D,且经过A(1,0);B(0,2) 两点,将△OAB绕点A顺时针旋转90后,点B落到点C的位置,将该抛物线沿着对称轴上下平移,使之经过点C,此时得到的新抛物线与y轴的交点为B1,顶点为D.
(1)求新抛物线的解析式;
(2)若点N在新抛物线上,满足三角形NBB1的面积是三角形NDD1面积的2倍,求点N坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com