
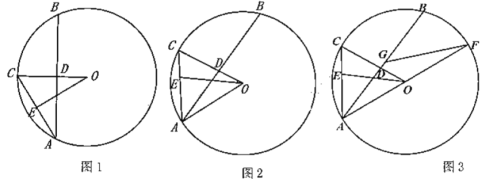
【题目】已知:![]() 、
、![]() 是圆
是圆![]() 中的两条弦,连接
中的两条弦,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() .
.
(1)如图1,若![]() ,求证:弧
,求证:弧![]()
![]() 弧
弧![]() ;
;
(2)如图2,连接![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,在第(2)问的条件下,延长![]() 交圆
交圆![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
科目:初中数学 来源: 题型:
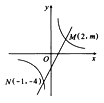
【题目】如图:一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于M、N两点
的图象交于M、N两点
(1)求反比例函数和一次函数的关系式;
(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
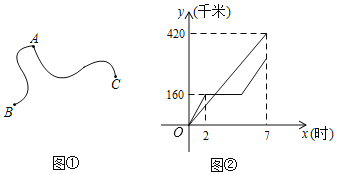
【题目】如图①,甲、乙两车同时从A地出发,分别匀速前往B地与C地,甲车到达B地休息一段时间后原速返回,乙车到达C地后立即返回.两车恰好同时返回A地.图②是两车各自行驶的路程y(千米)与出发时间x(时)之间的函数图象.根据图象解答下列问题:
(1)甲车到达B地休息了 时;
(2)求甲车返回A地途中y与x之间的函数关系式;
(3)当x为何值时,两车与A地的路程恰好相同.(不考虑两车同在A地的情况)
查看答案和解析>>
科目:初中数学 来源: 题型:
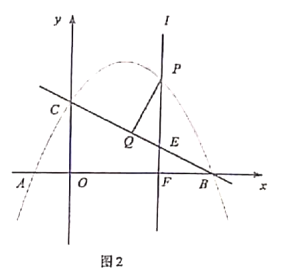
【题目】如图1,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
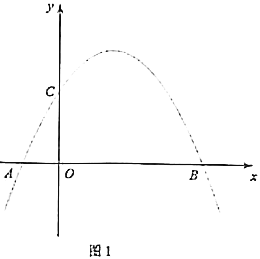
(1)求抛物线的表达式;
(2)点![]() 为抛物线的顶点,在
为抛物线的顶点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)如图2,位于![]() 轴右侧且垂直于
轴右侧且垂直于![]() 轴的动直线
轴的动直线![]() 沿
沿![]() 轴正方向从
轴正方向从![]() 运动到
运动到![]() (不含
(不含![]() 点和
点和![]() 点),分别与抛物线、直线
点),分别与抛物线、直线![]() 以及
以及![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元作为固定投资. 已知生产每件产品的成本是40元,在销售过程中发现:当销售单价定为120元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为![]() (元),年销售量为
(元),年销售量为![]() (万件),年获利为
(万件),年获利为![]() (万元)。(年获利=年销售额—生产成本—投资)
(万元)。(年获利=年销售额—生产成本—投资)
(1)试写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)请通过计算说明,到第一年年底,当![]() 取最大值时,销售单价
取最大值时,销售单价![]() 定为多少?此时公司是盈利了还是亏损了?
定为多少?此时公司是盈利了还是亏损了?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,点
,点![]() 在线段
在线段![]() 上,以
上,以![]() 为直径的⊙D经过点
为直径的⊙D经过点![]() .
.
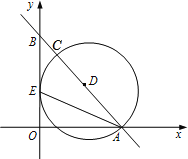
(1)判断⊙D与![]() 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
(2)求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
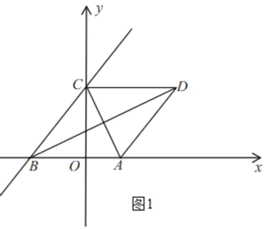
【题目】如图,在平面直角坐标系中,一次函数y=![]() x+4的图象与x轴交于点B,与y轴交于点C,二次函数y=
x+4的图象与x轴交于点B,与y轴交于点C,二次函数y=![]() x2+bx+c的图象经过点A(2,0)和点C,抛物线与x轴交于点A和点E(点A在点E的左侧),连接AC,将△ABC沿AC折叠,得到点B的对应点为点D.
x2+bx+c的图象经过点A(2,0)和点C,抛物线与x轴交于点A和点E(点A在点E的左侧),连接AC,将△ABC沿AC折叠,得到点B的对应点为点D.
(1)求二次函数的表达式;
(2)求点D坐标,并判定点D是否在该二次函数的图象上;
(3)①在线段AC上找一点F,使得△OBF的周长最小,直接写出此时点F的坐标.②在①的基础上,过点F的一条直线与抛物线对称轴右侧部分交于点N,交线段AD于点M,连接NA、ND,使△AMF与△AMN的面积比为4:1,请直接写出△AND的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了![]() 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com