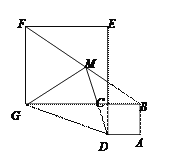
【题目】如图，正方形ABCD和正方形CEFG的面积分别为4 cm2,36cm2, 点G,C,B在一条直线上，M是BF的中点，则点M到GD的距离为_________cm．
【答案】
【解析】解：如图，作MK⊥DG于K，CN⊥DG于N，FH⊥DG于H，BT⊥DG于T．
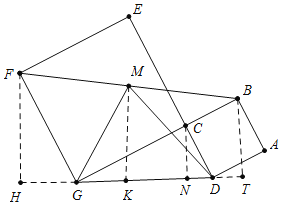
∵正方形ABCD和正方形CEFG的面积分别为4平方厘米和36平方厘米，∴FG=CG=6cm，CD=CB=2cm，∠FGC=∠GCD=∠H=∠CNG=90°，∴∠FGH+∠HFG=90°，∠FGH+∠CGN=90°，∴∠HFG=∠CGN．在△FGH和△GCN中，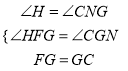 
，∴△FGH≌△GCN，∴FH=GN．在Rt△GCD中，DG=
=2
cm，CN=
=
cm，∴FH=GN=
=
=
cm．∵CN∥BT，∴
=
，∴
=
，∴BT=
cm．∵FM=MB，MK∥FH∥BT，∴KH=KT，∴MK=
=
cm．
故答案为： 
．
三新快车金牌周周练系列答案科目：初中数学 来源： 题型：
【题目】我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并规定：F（n）=
，例如12可以分解成1×12,2×6或3×4，因为12-1＞6-2＞4-3，所有3×4是最佳分解，所以F（12）=
.
（1）如果一个正整数a是另外一个正整数b的平方，我们称正整数a是完全平方数，求证：对任意一个完全平方数m，总有F（m）=1.
（2）如果一个两位正整数t，t=10x+y（1≤x≤y≤9,x,y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数t为“吉祥数”，求所有“吉祥数”中F（t）的最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD的外侧作等腰△ABE，AE=BE，连接ED、EC．
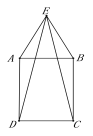
（1）求证：ED=EC．
（2）用无刻度的直尺作出△EDC中DC边上的高EH.（不写作法，保留作图的痕迹）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将长方形ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，已知∠BDC=62°，则∠DFE的度数为（ ）
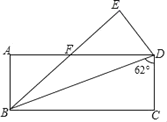
A. 62°B. 56°C. 31°D. 28°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，直线
（
）与直线
相交于点P（2，m），与x轴交于点A．
（1）求m的值；
（2）过点P作PB⊥x轴于B，如果△PAB的面积为6，求k的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某出租车司机从公司出发，在东西方向的人民路上连续接送5批客人，行驶路程记录如下(规定向东为正，向西为负，单位：km)：
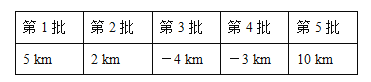
（1）接送完第5批客人后，该驾驶员在公司什么方向，距离公司多少千米？
（2）若该出租车每千米耗油0.2升，那么在这过程中共耗油多少升？
（3）若该出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按每千米加1.8元收费，在这过程中该驾驶员共收到车费多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，已知点A,B,C 在数轴上，对应表示的数是a,b,c.
（1）填空：A、B 之间的距离为 ；B、C 之间的距离为 ；A、C 之间的距离为 ；
（2）化简：|a+b|-|c-b|-|b-a|+|c|
（3）若 c2=9,-b 的倒数是它本身，a 的绝对值是 2，求（2a+b）-(c-b)-（a+2b-3c）的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，菱形OABC的顶点A在x轴的正半轴上，反比例函数y=
的图象经过点C（3，m）．
（1）求菱形OABC的周长；
（2）求点B的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义新运算：对于任意实数a，b，都有a⊕b=a（a﹣b）+1，等式右边是通常的加法，减法及乘法运算．比如：2⊕5=2×（2﹣5）+1=2×（﹣3）+1=﹣6+1=﹣5
（1）求3⊕（﹣2）的值；
（2）若3⊕x的值小于16，求x的取值范围，并在数轴上表示出来．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com