
【题目】在平面直角坐标系xOy中,已知点A(a,a),B(a,a﹣3),其中a为整数.点C在线段AB上,且点C的横纵坐标均为整数.
(1)当a=1时,画出线段AB;
(2)若点C在x轴上,求出点C的坐标;
(3)若点C纵坐标满足![]() ,直接写出a的所有可能取值: .
,直接写出a的所有可能取值: .
科目:初中数学 来源: 题型:
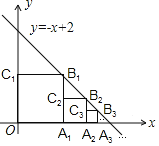
【题目】正方形![]() 、
、![]() 、
、![]() …按如图放置,其中点
…按如图放置,其中点![]() 、
、![]() 、
、![]() …在
…在![]() 轴正半轴上,点
轴正半轴上,点![]() 、
、![]() 、
、![]() …在直线
…在直线![]() 上,依此类推…,则点
上,依此类推…,则点![]() 的坐标是________;点
的坐标是________;点![]() 的坐标是_________.
的坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
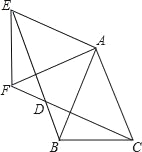
【题目】如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D
(1)求证:BE=CF;
(2)当四边形ACDE为平行四边形时,求证:△ABE为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的柑橘,物价部门规定每箱售价不得高于55元;市场调查发现,若每箱以45元的价格销售,平均每天销售105箱;每箱以50元的价格销售,平均每天销售90箱.假定每天销售量y(箱)与销售价x(元/箱)之间满足一次函数关系式.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里有5个小球,分别标有数字﹣3,﹣2,﹣1,﹣![]() ,﹣
,﹣![]() ,这些小球除所标的数不同外其余都相同,先从盒子随机摸出1个球,记下所标的数,再从剩下的球中随机摸出1个球,记下所标的数.
,这些小球除所标的数不同外其余都相同,先从盒子随机摸出1个球,记下所标的数,再从剩下的球中随机摸出1个球,记下所标的数.
(1)用画树状图或列表的方法求两次摸出的球所标的数之积不大于1的概率.
(2)若以第一次摸出球上的数字为横坐标,第二次摸出球上的数字为纵坐标确定一点,直接写出该点在双曲线y=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x.
(1)在给定的平面直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y<0时,x的取值范围;
(3)若将此图象沿x轴向左平移3个单位,再沿y轴向下平移1个单位,请直接写出平移后图象所对应的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com