
分析 画出函数y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的图象,要使直线y=kx+$\frac{1}{2}$(k>0)与函数y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的图象有且只有2个交点,只需直线经过(2,3)和经过(2,$\frac{1}{2}$)之间.
解答 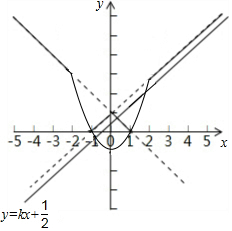 解:函数y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的图象如图所示
解:函数y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的图象如图所示
∵直线y=kx+$\frac{1}{2}$(k>0)与函数y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的图象有且只有2个交点,
当直线y=kx+$\frac{1}{2}$(k>0)经过点(2,3)时,则3=2k+$\frac{1}{2}$,
解得k=$\frac{5}{4}$,
当直线y=kx+$\frac{1}{2}$(k>0)经过点(-1,0)时,k=$\frac{1}{2}$,
当k=1时,平行于y=x+1,与函数y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的图象也有且仅有两个交点;
∴直线y=kx+$\frac{1}{2}$(k>0)与函数y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的图象有且只有2个交点,则k的取值为$\frac{1}{2}$<k≤1或k=$\frac{5}{4}$.
故答案为$\frac{1}{2}$<k≤1或k=$\frac{5}{4}$.
点评 本题考查了一次函数的性质以及一次函数的图象和二次函数的图象,数形结合思想的应用是解题的关键.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:选择题
| 时间(s) | 0 | 5 | 10 | 15 |
| 食用油温度(℃) | 20 | 35 | 50 | 65 |
| A. | 85℃ | B. | 120℃ | C. | 150℃ | D. | 170℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=$\frac{k}{x}$(x<0)的图象过点P,则k的值为( )
如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=$\frac{k}{x}$(x<0)的图象过点P,则k的值为( )| A. | -28 | B. | -20 | C. | 28 | D. | 26 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
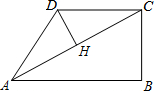 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )| A. | 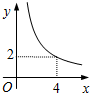 | B. | 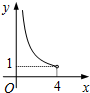 | C. | 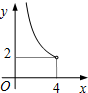 | D. | 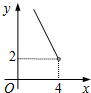 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
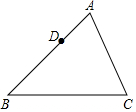 如图,已知锐角△ABC,点D是AB边上的一定点,请用尺规在AC边上求作一点E,使△ADE与△ABC相似.(作出符合题意的一个点即可,保留作图痕迹,不写作法.)
如图,已知锐角△ABC,点D是AB边上的一定点,请用尺规在AC边上求作一点E,使△ADE与△ABC相似.(作出符合题意的一个点即可,保留作图痕迹,不写作法.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com