

���� ��1����ͼ1����֤����ABCΪ�ȱ������εõ���ACB=��ABC=60�㣬AB=BC����֤����D=��DCE=30�㣬Ȼ����ݵ��������ε��ж������õ���CEDΪ���������Σ�
��2���ӳ�CF��MʹFM=CF������AM����ͼ2����֤����AMF�ա�BCF�õ�AM=BC����M=��BCF����֤����AMC�ա�BDA�õ���M=��D�����ԡ�D=��DCE�����ǿ��жϡ�CEDΪ���������Σ�
��3����BH��CE��H������BE����ͼ3���ɣ�2���á�CEDΪ���������Σ�����BCE=45��ʱ����CEDΪ����ֱ�������Σ���EB��CD����BH=x����CH=EH=x��BC=$\sqrt{2}$x����֤�á�AEF�ա�BHF����EF=HF=$\frac{1}{2}$HE=$\frac{1}{2}$x�������ù��ɶ��������BF=$\frac{\sqrt{5}}{2}$x������AB=2BF=$\sqrt{5}$x��Ȼ������$\frac{AB}{BC}$��ֵ��
��� ��1��֤������ͼ1��
��AB=AC����BAC=60�㣬
���ABCΪ�ȱ������Σ�
���ACB=��ABC=60�㣬AB=BC��
��BC=BD��
��AB=BD��
���D=��BAD��
����ABC=��D+��BAD��
���D=30�㣬
��F��AB���е㣬
��CFƽ�֡�ACB��
���ACE=��DCE=30�㣬
���D=��DCE��
���CED����������
��2���⣺������
�ӳ�CF��MʹFM=CF������AM����ͼ2��
�ڡ�AMF�͡�BCF��
$\left\{\begin{array}{l}{AF=BF}\\{��AFM=��BFC}\\{MF=CF}\end{array}\right.$��
���AMF�ա�BCF��
��AM=BC����M=��BCF��
��BC=BD��
��AM=BD��
�ߡ�M=��BCF��
��AM��CD��
���MAC+��ACB=180�㣬
����DBA+��ABC=180�㣬��ABC=��ACB��
���MAC=��DBA��
�ڡ�AMC�͡�BDA��
$\left\{\begin{array}{l}{AM=BD}\\{��MAC=��DBA}\\{AC=BA}\end{array}\right.$��
���AMC�ա�BDA��
���M=��D��
���D=��DCE��
���CED����������
��3���⣺��BH��CE��H������BE����ͼ3��
�ɣ�2���á�CEDΪ���������Σ�����BCE=45��ʱ����CEDΪ����ֱ�������Σ�
��EB��CD��
��BH=x����CH=EH=x��BC=$\sqrt{2}$x��
��֤�á�AEF�ա�BHF����EF=HF=$\frac{1}{2}$HE=$\frac{1}{2}$x��
�ڡ�BFH�У�BF=$\sqrt{{x}^{2}+��\frac{1}{2}x��^{2}}$=$\frac{\sqrt{5}}{2}$x��
��AB=2BF=$\sqrt{5}$x��
��$\frac{AB}{BC}$=$\frac{\sqrt{5}x}{\sqrt{2}x}$=$\frac{\sqrt{10}}{2}$��
�ʴ�Ϊ$\frac{\sqrt{10}}{2}$��
���� ���⿼�����������ۺ��⣺�������յ��������Ρ�����ֱ�������ε��ж������ʺ�ȫ�������ε��ж������ʣ������2��С��Ĺؼ�����ȫ��������֤������ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
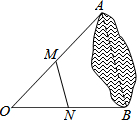 ��ͼ��Ϊ���Ƴ���������A��B�����ľ��룬�ڳ�����һ��ѡȡ��O���ֱ�ȡOA��OB���е�M��N�����MN=39m����A��B�����ľ�����78m��
��ͼ��Ϊ���Ƴ���������A��B�����ľ��룬�ڳ�����һ��ѡȡ��O���ֱ�ȡOA��OB���е�M��N�����MN=39m����A��B�����ľ�����78m���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
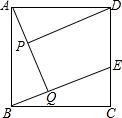 ��֪����ͼ����������ABCD�У���E�ڱ�CD�ϣ�AQ��BE�ڵ�Q��DP��AQ�ڵ�P����֤��AP=BQ��
��֪����ͼ����������ABCD�У���E�ڱ�CD�ϣ�AQ��BE�ڵ�Q��DP��AQ�ڵ�P����֤��AP=BQ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com