
| AC |
| AO |
| BD |
| DO |
| CP |
| PB |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 5 |
| 15 |
| 2 |
| 15 |
| 2 |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |

| 1 |
| 2 |
| AC |
| AO |
| 1 |
| 2 |
| BD |
| DO |
| 3 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2 |
| a |
| b |
| ||
| 1 |
| 1 |
| 2 |
| 1 |
| 3 |
| a |
| b |
| ||
| 1 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 5 |
| a |
| b |
| ||
|
| 15 |
| 2 |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
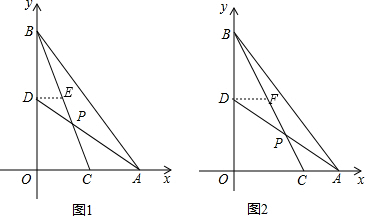 НтЃКЃЈ1ЃЉШчЭМ1ЃЌзїDEЁЮOAНЛBCгкЕуEЃЌ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌзїDEЁЮOAНЛBCгкЕуEЃЌ| AC |
| AO |
| BD |
| DO |
| 1 |
| 2 |
| AC |
| AO |
| 1 |
| 2 |
| BD |
| DO |
| 1 |
| 2 |
| 1 |
| 2 |
| DE |
| AC |
| EP |
| PC |
| EP |
| PC |
| 1 |
| 2 |
| CP |
| PB |
| 2PE |
| 4PE |
| 1 |
| 2 |
| CP |
| PB |
| 1 |
| 2 |
| AC |
| AO |
| BD |
| DO |
| 1 |
| 3 |
| AC |
| AO |
| 1 |
| 3 |
| BD |
| DO |
| 1 |
| 2 |
| DF |
| AC |
| PF |
| PC |
| CP |
| PB |
| CP |
| 3CP |
| 1 |
| 3 |
| CP |
| PB |
| CP |
| PB |
| 1 |
| 3 |
| 1 |
| 3 |
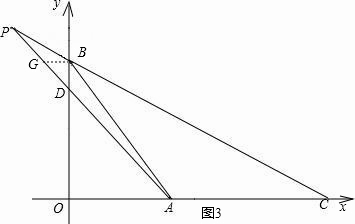 ШчЭМ3ЃЌзїGBЁЮOCНЛPAгкЕуGЃЌ
ШчЭМ3ЃЌзїGBЁЮOCНЛPAгкЕуGЃЌ| GB |
| OA |
| DB |
| DO |
| CP |
| PB |
| AC |
| GB |
| AC |
| AO |
| BD |
| DO |
| 3 |
| 2 |
| 1 |
| 5 |
| AC |
| AO |
| 3 |
| 2 |
| BD |
| DO |
| 1 |
| 5 |
| GB |
| OA |
| 1 |
| 5 |
| 3 |
| 2 |
| 15 |
| 2 |
| CP |
| PB |
| ||
| GB |
| 15 |
| 2 |
| CP |
| PB |
| 15 |
| 2 |
| 1 |
| 2 |
| a |
| b |
| ||
| 1 |
| 1 |
| 2 |
| 1 |
| 3 |
| a |
| b |
| ||
| 1 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 5 |
| a |
| b |
| ||
|
| 15 |
| 2 |
| a |
| b |
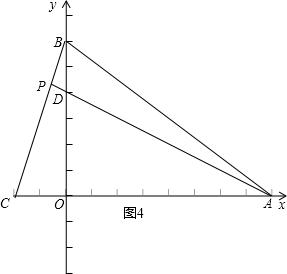 ЂкШчЭМ4ЃЌЁпADЕФНтЮіЪНy=-
ЂкШчЭМ4ЃЌЁпADЕФНтЮіЪНy=-| 1 |
| 2 |
| AC |
| AO |
| BD |
| DO |
| 10 |
| 8 |
| 5 |
| 4 |
| 2 |
| 4 |
| 1 |
| 2 |
| a |
| b |
| ||
|
| 5 |
| 2 |
| 15 |
| 2 |
| a |
| b |
| 5 |
| 2 |



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКОЋБрНЬВФШЋНтЁЁЪ§бЇЁЁОХФъМЖЩЯВсЁЁ(ХфЫеПЦАц) ЫеПЦАц ЬтаЭЃК047
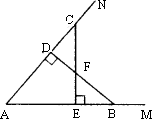
ШчЭМЃЌвбжЊЃКЕуBЁЂCЗжБ№дкЁЯMANЕФСНБпЩЯЃЌBDЁЭANЃЌCEЁЭAMЃЌДЙзуЗжБ№ЮЊDЁЂEЃЌBDЁЂCEЯрНЛгкЕуFЃЌЧвBFЃНCFЃЎ
ЧѓжЄЃКЕуFдкЁЯMANЕФЦНЗжЯпЩЯЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2012НьеуНЖЋбєЮтгюГѕМЖжабЇжаПМФЃФтЪ§бЇЪдОэЃЈДјНтЮіЃЉ ЬтаЭЃКНтД№Ьт
вбжЊЃКЕуAЁЂBЗжБ№дкжБНЧзјБъЯЕЕФxЁЂyжсЕФе§АыжсЩЯЃЌOЪЧзјБъдЕуЃЌЕуCдкЩфЯпAOЩЯЃЌЕуDдкЯпЖЮOBЩЯЃЌжБЯпADгыЯпЖЮBCЯрНЛгкЕуPЃЌЩш=aЃЌ =bЃЌ=kЁЃ
ЃЈ1ЃЉШчЭМ1ЃЌЕБa=ЃЌb=1ЪБЃЌЧыЧѓГіkЕФжЕЃЛ
ЃЈ2ЃЉЕБa=ЃЌb=1ЪБ(ШчЭМ2)ЃЌЧыЧѓГіkЕФжЕЃЛЕБa=ЃЌb=ЪБЃЌk=ЁјЃЛ
ЃЈ3ЃЉИљОнвдЩЯЬНЫїбаОПЃЌЧыФуНтОівдЯТЮЪЬтЃКЂйЧыжБНгаДГігУКЌaЃЌbДњЪ§ЪНБэЪОk=ЁјЃЛЂк ШєЕуA(8,0)ЃЌЕуBЃЈ0ЃЌ6ЃЉЃЌCЃЈЃ2ЃЌ0ЃЉЃЌжБЯпADЮЊЃКy=Ѓx+4ЃЌдђk=ЁјЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2012ФъеуНЪЁН№ЛЊЪажаПМЪ§бЇФЃФтЪдОэЃЈЦпЃЉЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
 =aЃЌ
=aЃЌ =bЃЌ
=bЃЌ =kЃЎ
=kЃЎ ЃЌb=1ЪБЃЌЧыЧѓГіkЕФжЕЃЛ
ЃЌb=1ЪБЃЌЧыЧѓГіkЕФжЕЃЛ ЃЌb=1ЪБЃЈШчЭМ2ЃЉЃЌЧыЧѓГіkЕФжЕЃЛЕБa=
ЃЌb=1ЪБЃЈШчЭМ2ЃЉЃЌЧыЧѓГіkЕФжЕЃЛЕБa= ЃЌb=
ЃЌb= ЪБЃЌk=______ЃЛ
ЪБЃЌk=______ЃЛ x+4ЃЌдђk=______ЃЎ
x+4ЃЌдђk=______ЃЎ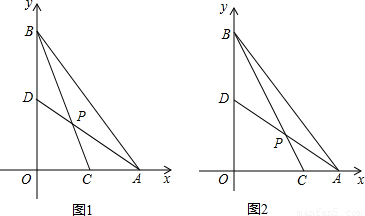
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2011-2012бЇФъеуНЖЋбєЮтгюГѕМЖжабЇжаПМФЃФтЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
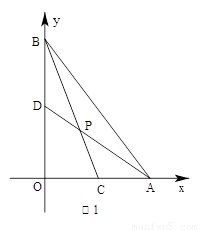
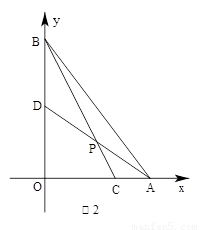
вбжЊЃКЕуAЁЂBЗжБ№дкжБНЧзјБъЯЕЕФxЁЂyжсЕФе§АыжсЩЯЃЌOЪЧзјБъдЕуЃЌЕуCдкЩфЯпAOЩЯЃЌЕуDдкЯпЖЮOBЩЯЃЌжБЯпADгыЯпЖЮBCЯрНЛгкЕуPЃЌЩш=aЃЌ =bЃЌ=kЁЃ
ЃЈ1ЃЉШчЭМ1ЃЌЕБa=ЃЌb=1ЪБЃЌЧыЧѓГіkЕФжЕЃЛ
ЃЈ2ЃЉЕБa=ЃЌb=1ЪБ(ШчЭМ2)ЃЌЧыЧѓГіkЕФжЕЃЛЕБa=ЃЌb=ЪБЃЌk= ЁјЃЛ
ЃЈ3ЃЉИљОнвдЩЯЬНЫїбаОПЃЌЧыФуНтОівдЯТЮЪЬтЃКЂйЧыжБНгаДГігУКЌaЃЌbДњЪ§ЪНБэЪОk=ЁјЃЛЂк ШєЕуA(8,0)ЃЌЕуBЃЈ0ЃЌ6ЃЉЃЌCЃЈЃ2ЃЌ0ЃЉЃЌжБЯпADЮЊЃКy=Ѓx+4ЃЌдђk=ЁјЁЃ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com