
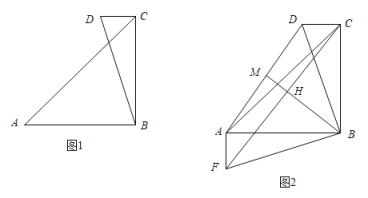
【题目】如图,![]() 与
与![]() 在线段
在线段![]() 的同侧,
的同侧,![]() ,
,![]() .
.
(1)如图![]() ,已知
,已知![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,点
,点![]() 、
、![]() 的对应点分别是点
的对应点分别是点![]() 、
、![]() ,连接
,连接![]() 和
和![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)在Rt△ABC中,利用特殊角的三角函数值求得BC的长,然后在Rt△BCD中,利用勾股定理即可求得答案;
(2)先根据旋转的性质得到∠AFB=∠BDC,∠FAB=∠DCB=90°,BF=BD,BC=AB,进而推出AF∥BC,再根据平行线的性质的性质得到∠FBC =∠BDQ,则通过“角角边”证明△FBC≌△BDQ,得到FC=BQ,BC=DQ,再通过“角角边”证明△ABM≌△DQM,得到BM=MQ=![]() BQ=
BQ=![]() FC,即可得证.
FC,即可得证.
解(1)∵△ABC为直角三角形,且AB=BC,
∴△ABC为等腰直角三角形,
∴BC=AC·sin45°=6![]() ·
·![]() =6,
=6,
在Rt△BCD中,
CD=![]() =
=![]() =
=![]() ;
;
(2)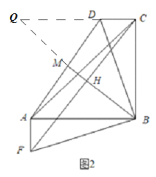
如图,分别延长BM、CD交于点Q,
∵∠BCQ=90°,BH⊥EC,
∴∠Q=∠BCH,
又∵将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,
∴∠AFB=∠BDC,∠FAB=∠DCB=90°,BF=BD,BC=AB,
∵∠ABC=90°,
∴AF∥BC,
∴∠FBC=180°﹣∠AFB=180°﹣∠BDC=∠BDQ,
∴△FBC≌△BDQ(AAS),
∴FC=BQ,BC=DQ,
∵BC=AB,
∴DQ=AB,
∵AB∥CD,
∴∠BAD=∠QDA,
∴△ABM≌△DQM(AAS),
∴BM=MQ=![]() BQ=
BQ=![]() FC,
FC,
∴CF=2BM.


科目:初中数学 来源: 题型:
【题目】下面是“经过圆外一点作圆的切线”的尺规作图的过程.
已知:P为外一点.求作:经过P点的切线.作法:如图,(1)连结OP;(2)以OP为直径作圆,与交于C、D两点.(3)作直线PC、PD.则直线PC、PD就是所求作经过P点的切线.以上作图的依据是:_____.
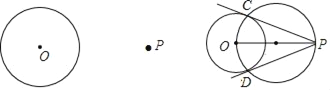
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
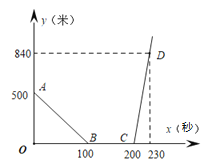
【题目】小明和妈妈开车去中央公园采风,小明爸爸发现他们忘记带画笔后立即开车追赶他们.假设妈妈和爸爸的车在同一直线公路上匀速行驶,当爸爸的车追上妈妈的车后,两车停下来,爸爸把画笔交给小明.然后小明和妈妈开车以原来速度的![]() 倍继续前行,爸爸则以来时一半的速度沿原路回家.设小明爸爸开车的时间为
倍继续前行,爸爸则以来时一半的速度沿原路回家.设小明爸爸开车的时间为![]() (秒),两车间的距离为
(秒),两车间的距离为![]() (米),
(米),![]() 关于
关于![]() 的部分函数关系如图所示,当小明爸爸回到家时,小明和妈妈正好行驶了全程的
的部分函数关系如图所示,当小明爸爸回到家时,小明和妈妈正好行驶了全程的![]() ,则小明家离中央公园的距离为________米
,则小明家离中央公园的距离为________米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2;以此进行下去…,则正方形A2019B2019C2019D2019的面积为( )

A.52017B.52018C.52019D.52020
查看答案和解析>>
科目:初中数学 来源: 题型:
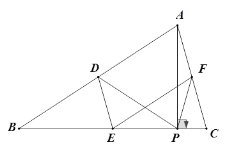
【题目】如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AP是边BC上的高
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DEF=∠DPF
查看答案和解析>>
科目:初中数学 来源: 题型:
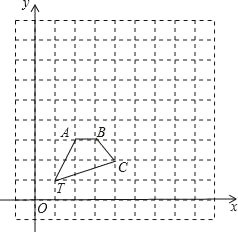
【题目】如图,在正方形网格中,四边形TABC的顶点坐标分别为T(1,1),A(2,3),B(3,3),C(4,2).
(1)以点T(1,1)为位似中心,在位似中心的同侧将四边形TABC放大为原来的2倍,放大后点A,B,C的对应点分别为A′,B′,C′画出四边形TA′B′C′;
(2)写出点A′,B′,C′的坐标:
A′ ,B′ ,C′ ;
(3)在(1)中,若D(a,b)为线段AC上任一点,则变化后点D的对应点D′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=﹣x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点B的坐标为(﹣1,0)
(1)求抛物线的解析式并作出图象;
(2)点D的坐标为(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com