
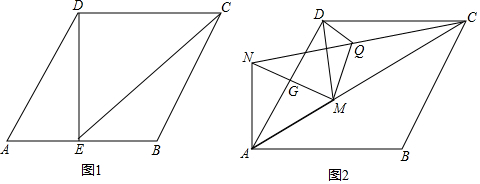
分析 (1)如图1,连接对角线BD,先证明△ABD是等边三角形,根据E是AB的中点,由等腰三角形三线合一得:DE⊥AB,利用勾股定理依次求DE和EC的长;
(2)如图2,作辅助线,构建全等三角形,先证明△ADH是等边三角形,再由△AMN是等边三角形,得条件证明△ANH≌△AMD(SAS),则HN=DM,根据DQ是△CHN的中位线,得HN=2DQ,由等量代换可得结论.
解答 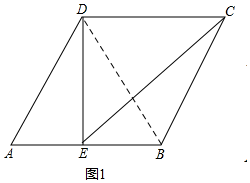 解:(1)如图1,连接BD,则BD平分∠ABC,
解:(1)如图1,连接BD,则BD平分∠ABC,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=60°,
∴∠ABC=120°,
∴∠ABD=$\frac{1}{2}$∠ABC=60°,
∴△ABD是等边三角形,
∴BD=AD=4,
∵E是AB的中点,
∴DE⊥AB,
由勾股定理得:DE=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵DC∥AB,
∴∠EDC=∠DEA=90°,
在Rt△DEC中,DC=4,
EC=$\sqrt{D{C}^{2}+D{E}^{2}}$=$\sqrt{{4}^{2}+(2\sqrt{3})^{2}}$=2$\sqrt{7}$;
(2)如图2,延长CD至H,使CD=DH,连接NH、AH,
∵AD=CD,
∴AD=DH,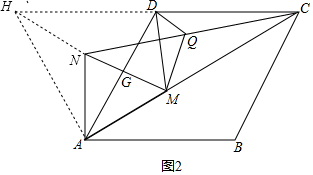
∵CD∥AB,
∴∠HDA=∠BAD=60°,
∴△ADH是等边三角形,
∴AH=AD,∠HAD=60°,
∵△AMN是等边三角形,
∴AM=AN,∠NAM=60°,
∴∠HAN+∠NAG=∠NAG+∠DAM,
∴∠HAN=∠DAM,
在△ANH和△AMD中,
∵$\left\{\begin{array}{l}{AH=AD}\\{∠HAN=∠DAM}\\{AN=AM}\end{array}\right.$,
∴△ANH≌△AMD(SAS),
∴HN=DM,
∵D是CH的中点,Q是NC的中点,
∴DQ是△CHN的中位线,
∴HN=2DQ,
∴DM=2DQ.
点评 本题考查了菱形的性质、三角形的中位线、三角形全等的性质和判定、等边三角形的性质和判定,本题证明△ANH≌△AMD是关键,并与三角形中位线相结合,解决问题;第二问有难度,注意辅助线的构建.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
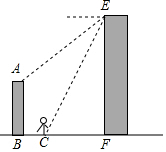 为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工在塔EF的顶部处测得对面一栋AB=9米高的楼房顶部A的俯角为45°,测得楼房正前方BC=7米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?($\sqrt{3}$≈1.732,结果保留到1米.)
为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工在塔EF的顶部处测得对面一栋AB=9米高的楼房顶部A的俯角为45°,测得楼房正前方BC=7米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?($\sqrt{3}$≈1.732,结果保留到1米.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
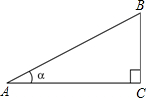 如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=$\frac{角α的邻边}{角α的对边}$=$\frac{AC}{BC}$,根据上述角的余切定义,解下列问题:
如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=$\frac{角α的邻边}{角α的对边}$=$\frac{AC}{BC}$,根据上述角的余切定义,解下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
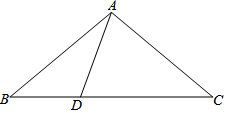 在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.
在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
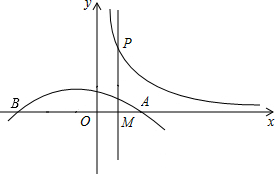 如图,抛物线L:y=-$\frac{1}{2}$(x-1)(x+3)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=8.
如图,抛物线L:y=-$\frac{1}{2}$(x-1)(x+3)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com