
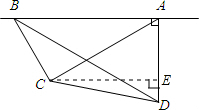
 (2013•石景山区一模)如图,一架飞机由A向B沿水平直线方向飞行,在航线AB的正下方有两个山头C、D.飞机在A处时,测得山头D恰好在飞机的正下方,山头C在飞机前方,俯角为30°.飞机飞行了6千米到B处时,往后测得山头C、D的俯角分别为60°和30°.已知山头D的海拔高度为1千米,求山头C的海拔高度.(精确到0.01千米,已知
(2013•石景山区一模)如图,一架飞机由A向B沿水平直线方向飞行,在航线AB的正下方有两个山头C、D.飞机在A处时,测得山头D恰好在飞机的正下方,山头C在飞机前方,俯角为30°.飞机飞行了6千米到B处时,往后测得山头C、D的俯角分别为60°和30°.已知山头D的海拔高度为1千米,求山头C的海拔高度.(精确到0.01千米,已知| 3 |
| ||
| 3 |
| 3 |
| ||
| 2 |
| 3 |
3
| ||
| 2 |
| 3 |
3
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1.732 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
(2013•石景山区二模)一射击运动员在一次射击练习中打出的成绩如下表所示:这次成绩的众数、平均数是( )
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com