
【题目】如图1,![]() 于点
于点![]() ,
,![]() .
.
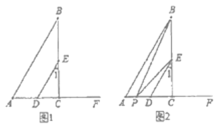
(1)求证:![]() ;
;
(2)如图2,点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 运动到点
运动到点![]() 停止,连接
停止,连接![]() 、
、![]() .则
.则![]() 、
、![]() 、
、![]() 三个角之间具有怎样的数量关系(不考虑点
三个角之间具有怎样的数量关系(不考虑点![]() 与点
与点![]() ,
,![]() ,
,![]() 重合的情况)?并说明理由.
重合的情况)?并说明理由.
【答案】(1)见详解;(2)当点P在A,D之间时,![]() ;当点P在C,D之间时,
;当点P在C,D之间时,![]() ;当点P在C,F之间时,
;当点P在C,F之间时,![]() .
.
【解析】
(1)根据∠A+∠B=90°,∠A+∠1=90°,即可得到∠B=∠1,进而得出AB∥DE.
(2)分三种情况讨论:点P在A,D之间;点P在C,D之间;点P在C,F之间;分别过P作PG∥AB,利用平行线的性质,即可得到∠ABP,∠DEP,∠BPE三个角之间的数量关系.
解:(1)如图1,∵BC⊥AF于点C,
∴∠A+∠B=90°,
又∵∠A+∠1=90°,
∴∠B=∠1,
∴AB∥DE.
(2)如图2,当点P在A,D之间时,过P作PG∥AB,

∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠BPG+∠EPG=∠ABP+∠DEP;
∴![]() ;
;
如图所示,当点P在C,D之间时,过P作PG∥AB,
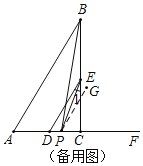
∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠BPG-∠EPG=∠ABP-∠DEP;
∴![]() ;
;
如图所示,当点P在C,F之间时,过P作PG∥AB,

∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠EPG-∠BPG=∠DEP-∠ABP.
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,结果为F(n)=3n+1;②当n为偶数时,结果为F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行.例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行.例如,取n=13,则:
![]()
若n=24,则第100次“F”运算的结果是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】字母m、n分别表示一个有理数,且m≠n.现规定min{m,n}表示m、n中较小的数,例如:min{3,﹣1}=﹣1,min{﹣1,0}=﹣1.据此解决下列问题:
(1)min{﹣![]() ,﹣
,﹣![]() }= .
}= .
(2)若min{![]() ,2)=﹣1,求x的值;
,2)=﹣1,求x的值;
(3)若min{2x﹣5,x+3}=﹣2,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)完成下面的证明(在括号中填写推理理由)如图,已知![]() ,
,![]() ,求证:
,求证:![]() .
.

证明:因为![]() ,
,
所以![]() (________),
(________),
所以![]() ________
________![]() (________).
(________).
因为![]() ,
,
所以![]() ________
________![]() (________).
(________).
所以![]() (________).
(________).
(2)如图,![]() 、
、![]() 、
、![]() 三点在同一直线上,
三点在同一直线上,![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
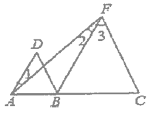
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学探究活动中:如图,在△ABC中,AB=5,AC=9,AD是BC边上的中线,
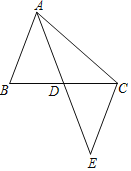
求AD的取值范围.小明给出了一种方法,步骤如下:
①过点C作一条与AB平行的线;
②延长AD交这条平行线于点E;
③通过证明得到AD=DE,AB=CE;
④利用△ACE三边的数量关系得到AD的取值范围.
根据这个方法,请你完成下面两个问题:
(1)求证:AD=DE,AB=CE;
(2)求AD的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乔亚萍和张红武做游戏,乔亚萍说:“你在心中想好一个两位数,对这个两位数进行如下的运算:①这个两位数的十位数字和个位数字相加,将所得的和乘以11;②用原两位数的十位数字减去个位数字,将所得的差乘以9;③用①中所得的结果减去②中所得的结果,所得的差加上16,得到最终的结果,把这个结果告诉我,我就能猜出你心中想的数了.”张红武算的结果为50,请帮乔亚萍算出张红武心中想的数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com