
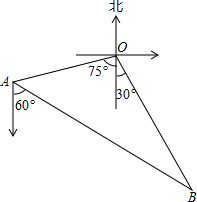
 如图,编号为2307和2308的两艘海监船同时从港口O出发外出某岛海域巡航,2307海监船沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,2308海监船沿南偏东30°方向以每小时15海里的速度航行,航行1小时后,2307海监船在A处收到消息,2308海监船附近发现疑似敌舰,于是2307海监船迅速改变航向和速度,以匀速沿南偏东60°方向追赶2308海监船,正好在B处追上,2307海监船追赶2308海监船的速度为多少海里/时?
如图,编号为2307和2308的两艘海监船同时从港口O出发外出某岛海域巡航,2307海监船沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,2308海监船沿南偏东30°方向以每小时15海里的速度航行,航行1小时后,2307海监船在A处收到消息,2308海监船附近发现疑似敌舰,于是2307海监船迅速改变航向和速度,以匀速沿南偏东60°方向追赶2308海监船,正好在B处追上,2307海监船追赶2308海监船的速度为多少海里/时? 分析 作OC⊥AB于C,根据题意求出∠OAB的度数,根据正弦和余弦的定义求出OC和AC的长,求出∠B的度数,根据正弦和正切的定义求出OB和BC的长,根据题意列出方程,解方程即可.
解答 解: 作OC⊥AB于C,
作OC⊥AB于C,
由题意得,∠AOD=75°,∠EAB=60°,
∴∠OAB=45°,又OA=15$\sqrt{2}$,
∴OC=AC=15,
∵∠OAB=45°,∠AOB=105°,
∴∠B=30°,又OC=15,
∴OB=3O,BC=15$\sqrt{3}$,
设2307海监船追赶2308海监船的速度为x海里/时,
由题意得,$\frac{15+15\sqrt{3}}{x}$=$\frac{30-15}{1}$,
解得x=$\sqrt{3}$+1.
答:2307海监船追赶2308海监船的速度为($\sqrt{3}$+1)海里/时.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、熟记锐角三角函数的概念是解题的关键.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:解答题
 已知A,B两地相距30km,甲骑自行车以15km/h的速度从A地到B地,同时,乙骑摩托车以30km/h的速度从B地到A地,到达A地后立即按原路原速返回,设甲、乙两人离B地的距离分别为y甲(km),y乙(km),行驶时间为t(h).
已知A,B两地相距30km,甲骑自行车以15km/h的速度从A地到B地,同时,乙骑摩托车以30km/h的速度从B地到A地,到达A地后立即按原路原速返回,设甲、乙两人离B地的距离分别为y甲(km),y乙(km),行驶时间为t(h).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
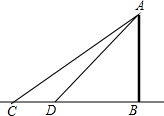 如图所示,对岸有一铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进16米到达D,在D处测得A的仰角为40°,求铁塔AB的高.(结果保留整数)
如图所示,对岸有一铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进16米到达D,在D处测得A的仰角为40°,求铁塔AB的高.(结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
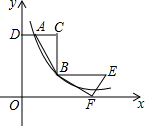 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,延长CA交y轴于点D,AD=1.
如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,延长CA交y轴于点D,AD=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com