
(1)阅读合作学习内容,请解答其中的问题;
(2)小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”
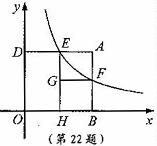 针对小亮提出的问题,请你判断这两个矩形能否全等?直接写出结论即可;这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由。
针对小亮提出的问题,请你判断这两个矩形能否全等?直接写出结论即可;这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由。
科目:初中数学 来源: 题型:
将抛物线y=x2-6x+5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
A.y=(x-4)2-6 B.y=(x-4)2-2 C.y=(x-2)2-2 D.y=(x-1)2-3
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某电信公司提供了A,B两种方案的移动通讯费用 (元)与通话时间
(元)与通话时间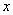 (元)之间的关系,则以下说法错误的是( )
(元)之间的关系,则以下说法错误的是( )
(A)若通话时间少于120分,则A方案比B方案便宜20元.
(B)若通话时间超过200分,则B方案比A方案便宜12元.
(C)若通讯费用为60元,则B方案比A方案的通话时间多.
(D)若两种方案通讯费用相差10元,则通话时间是145分或185分.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,直线 :
: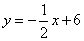 分别与
分别与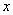 轴、
轴、 轴交于点B、C,且与直线
轴交于点B、C,且与直线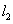 :
: 交于点A.
交于点A.
(1)分别求出点A、B、C的坐标;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com