
【题目】某校为了解七、八年级学生英语听力训练情况(七、八年级学生人数相同),某周从这两个年级学生中分别随机抽查了30名同学,调查了他们周一至周五的听力训练情况,根据调查情况得到如下统计图表:
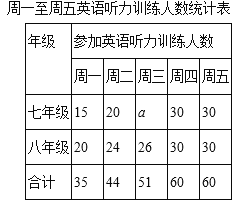

(1)填空:a= ;
(2)根据上述统计图表完成下表中的相关统计量:
年级 | 平均训练时间的中位数 | 参加英语听力训练人数的方差 |
七年级 | 24 | 34 |
八年级 |
| 14.4 |
(3)请你利用上述统计图表对七、八年级英语听力训练情况写出两条合理的评价;
(4)请你结合周一至周五英语听力训练人数统计表,估计该校七、八年级共480名学生中周一至周五平均每天有多少人进行英语听力训练.
【答案】(1)25;(2)27;(3)参加训练的学生人数超过一半;训练时间比较合理;(4)400人
【解析】
(1)由题意得:a=51﹣26=25;
(2)按照从小到大的顺序排列为:18、25、27、30、30,由中位数的定义即可得出结果;
(3)参加训练的学生人数超过一半;训练时间比较合理;
(4)求出抽查的七、八年级共60名学生中,周一至周五训练人数的平均数为50,用该校七、八年级共480名×周一至周五平均每天进行英语听力训练的人数所占比例即可.
解:(1)由题意得:a=51﹣26=25;
故答案为:25;
(2)按照从小到大的顺序排列为:18、25、27、30、30,
∴八年级平均训练时间的中位数为:27;
故答案为:27;
(3)参加训练的学生人数超过一半;训练时间比较合理;
(4)抽查的七、八年级共60名学生中,周一至周五训练人数的平均数为![]() (35+44+51+60+60)=50,
(35+44+51+60+60)=50,
∴该校七、八年级共480名学生中周一至周五平均每天进行英语听力训练的人数为480×![]() =400(人).
=400(人).


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点坐标为(1,2),那么下列结论中:①abc>0;②2a+b═0;③b2﹣4ac>0;④若关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,则m>2;⑤方程|ax2+bx+c|=1有四个根,则这四个根的和为4.正确的个数为( )
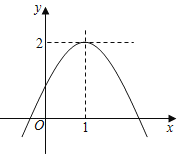
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l:y=kx+1(k≠0)与直线x=k,直线y=﹣k分别交于点A、B,直线x=k与直线y=﹣k交于点C,
(1)求直线l与y轴的交点坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段AB、BC、CA围成的区域(不含边界)为W.
①当k=1时,区域内的整点有 个,其坐标为 .
②当k=2时,区域W内的整点有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,它们的速度均为
匀速运动,它们的速度均为![]() .作
.作![]() 于
于![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() ,解答下列问题:
,解答下列问题:
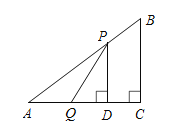
(1)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,
之间的函数关系式,![]() 的最大值是 ;
的最大值是 ;
(2)当![]() 的值为 时,
的值为 时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=x+4与y=kx+4分别交x轴于点A、B,两直线交于y轴上同一点C,点D的坐标为(﹣![]() ,0),点E是AC的中点,连接OE交CD于点F.
,0),点E是AC的中点,连接OE交CD于点F.
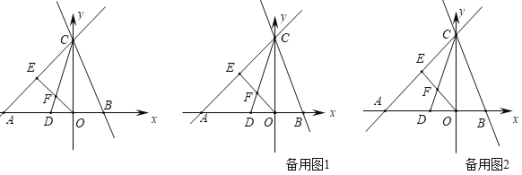
(1)求点F的坐标;
(2)若∠OCB=∠ACD,求k的值;
(3)在(2)的条件下,过点F作x轴的垂线1,点M是直线BC上的动点,点N是x轴上的动点,点P是直线l上的动点,使得以B,P,M、N为顶点的四边形是菱形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】木工师傅可以用角尺测量并计算出圆的半径r.用角尺的较短边紧靠⊙O,角尺的顶点B(∠B=90°),并使较长边与⊙O相切于点C.

(1)如图,AB<r,较短边AB=8cm,读得BC长为12cm,则该圆的半径r为多少?
(2)如果AB=8cm,假设角尺的边BC足够长,若读得BC长为acm,则用含a的代数式表示r为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校今年学生节期间准备销售一种成本为每瓶4元的饮料.据去年学生节试销情况分析,按每瓶5元销售,一天能售出500瓶;在此基础上,销售单价每涨0.1元,该日销售量就减少10瓶.针对这种饮料的销售情况,请解答以下问题:
(1)设销售单价为每瓶x元,当日销售量为y元,求y与x的函数关系式(不写出x的取值范围);
(2)设该日销售利润为w元,求w与x的函数关系式(不写出x的取值范围);
(3)该日销售利润为800元,求销售单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
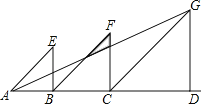
【题目】三个等腰直角三角形Rt△ABE,Rt△BCF,Rt△CDG如图摆放在射线AD上,直角顶点分别为B,C,D,已知相似比为2:3:4,AB=4,则(1)CG的长为_____;(2)图中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
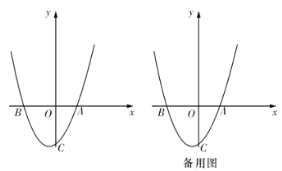
【题目】如图,已知抛物线![]()
![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于
轴相交于![]() 点,对称轴为
点,对称轴为![]() ,直线
,直线![]() 与抛物线相交于
与抛物线相交于![]() 、
、![]() 两点.
两点.
(1)求此抛物线的解析式;
(2)![]() 为抛物线上一动点,且位于
为抛物线上一动点,且位于![]() 的下方,求出
的下方,求出![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标;
的坐标;
(3)设点![]() 在
在![]() 轴上,且满足
轴上,且满足![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com