
【题目】计算
(1)2x(x+1)﹣(x+2)(x﹣2)+(x﹣1)2
(2)(x﹣1﹣ ![]() )
) ![]() .
.
【答案】
(1)解:原式=2x2+2x﹣x2+4+x2﹣2x+1=2x2+5
(2)解:原式= ![]()
![]() =
= ![]()
![]() =x+4
=x+4
【解析】(1)原式利用单项式乘以多项式,平方差公式,以及完全平方公式化简,去括号合并即可得到结果;(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
【考点精析】解答此题的关键在于理解分式的混合运算的相关知识,掌握运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]}.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
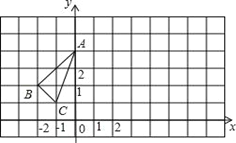
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于y轴对称的△ABlCl;
(2)点P在x轴上,且点P到点B与点C的距离之和最小,直接写出点P的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD中,AD=DC,∠DAB=∠ACB=90°,过点D作DF⊥AC,垂足为F.DF与AB相交于E.设AB=15,BC=9,P是射线DF上的动点.当△BCP的周长最小时,DP的长为 . 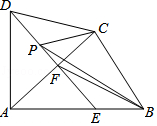
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D,F在x轴上,点C在DE边上,反比例函数y= ![]() (k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )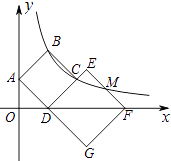
A.![]()
B.![]()
C.16
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C是直角,AB=6cm,∠ABC=60°,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的D处,则AC边扫过的图形众人阴影部分的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E是边BC的中点,连接AE并延长,交DC的延长线于点F,连接AC,BF.
(1)求证:△ABE≌△FCE;
(2)当四边形ABFC是矩形时,当∠AEC=80°,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.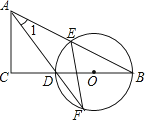
(1)求证:∠1=∠F.
(2)若sinB= ![]() ,EF=2
,EF=2 ![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合,研究数轴我们发现:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为![]() .如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为
.如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为![]() =3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
=3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)用含t的代数式表示:t秒后,点P表示的数为 ,点Q表示的数为 .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com