
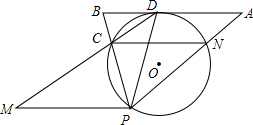
 如图,在⊙O中,弧DC=弧DN,点P为⊙O上一点,过D作CN的平行线交PN,PC的延长线于A,B,过P作PM∥AB交DC的延长线于M.
如图,在⊙O中,弧DC=弧DN,点P为⊙O上一点,过D作CN的平行线交PN,PC的延长线于A,B,过P作PM∥AB交DC的延长线于M.分析 (1)由$\widehat{DC}=\widehat{DN}$,得到OD⊥CN,再由AB∥CN即可,
(2)先判断出△DCP∽△DPM,得到$\frac{PD}{DM}=\frac{CD}{DP}$,再判断出△ADN∽△APD,得出AD=2AN,$\frac{AN}{AD}$=$\frac{DN}{PD}$即可;
(3)先判断出△DCP∽△DPM,得到$\frac{PD}{DM}=\frac{CD}{DP}$,再判断出△ADN∽△APD,得出AD=$\sqrt{m+1}$AN,$\frac{AN}{AD}$=$\frac{DN}{PD}$即可;
解答 (1)证明:如图,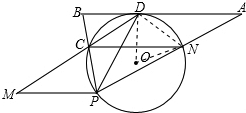
连接OD,
∵$\widehat{DC}=\widehat{DN}$,
∴OD⊥CN,
∵AB∥CN
∴OD⊥AB,
∵点D在⊙O上,
∴AB为⊙O切线.
(2)如图,
连接DN,
∵$\widehat{DC}=\widehat{DN}$,
∴∠DCN=∠CPD,CD=DN
∵PM∥AB,CN∥AB,
∴CN∥MP,
∴∠DCN=∠M,
∴∠DPC=∠M,
∵∠CDP=∠PDM,
∴△DCP∽△DPM,
∴$\frac{PD}{DM}=\frac{CD}{DP}$
∵∠DAN=∠PAD,∠ADN=∠APD,
∴△ADN∽△APD,
∴$\frac{AD}{AP}$=$\frac{AN}{AD}$=$\frac{DN}{PD}$,
∵PN=3AN,
∴AP=4AN,
∴AD2=AP×AN=4AN×AN,
∴AD=2AN,
∵$\frac{AN}{AD}=\frac{DN}{PD}=\frac{CD}{PD}=\frac{1}{2}$,
∴$\frac{PD}{DM}=\frac{1}{2}$;
(3)如图,
猜想$\frac{PD}{DM}$=$\frac{1}{\sqrt{m+1}}$,
理由:连接DN,
∵$\widehat{DC}=\widehat{DN}$,
∴∠DCN=∠CPD,DN=CD
∵PM∥AB,CN∥AB,
∴CN∥MP,
∴∠DCN=∠M,
∴∠DPC=∠M,
∵∠CDP=∠PDM,
∴△DCP∽△DPM,
∴$\frac{PD}{DM}=\frac{CD}{DP}$
∵∠DAN=∠PAD,∠ADN=∠APD,
∴△ADN∽△APD,
∴$\frac{AD}{AP}$=$\frac{AN}{AD}$,
∵PN=mAN,
∴AP=(m+1)AN,
∴AD2=AP×AN=(m+1)AN×AN,
∴AD=$\sqrt{m+1}$AN,
∵$\frac{AN}{AD}$=$\frac{DN}{PD}$=$\frac{CD}{PD}$=$\frac{1}{\sqrt{m+1}}$,
∴$\frac{PD}{DM}$=$\frac{1}{\sqrt{m+1}}$.
点评 此题是圆综合题,主要考查了垂径定理,相似三角形的性质和判定,切线的判定定理,解本题的关键是判断三角形相似.


科目:初中数学 来源: 题型:解答题
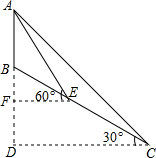 如图,山顶上有一信号塔AB,山坡BC的坡度为i=1:$\sqrt{3}$,现在为了测量塔高AB,测量人员选择山脚C处为一侧量点,测得塔顶仰角为45°,然后顺山坡向上行走100米到达E处,再测得塔顶仰角为60°,求塔高AB.
如图,山顶上有一信号塔AB,山坡BC的坡度为i=1:$\sqrt{3}$,现在为了测量塔高AB,测量人员选择山脚C处为一侧量点,测得塔顶仰角为45°,然后顺山坡向上行走100米到达E处,再测得塔顶仰角为60°,求塔高AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | -$\frac{2}{3}$ | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:当x>0时,反比例函数${y_1}=\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B.
已知:当x>0时,反比例函数${y_1}=\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=6,b=8,c=10 | B. | a=1,b=$\sqrt{2}$,c=$\sqrt{3}$ | C. | a=3,b=4,c=5 | D. | a=2,b=3,c=$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解某校初三一班的体育学考成绩 | B. | 了解某种节能灯的使用寿命 | ||
| C. | 了解我国青年人喜欢的电视节目 | D. | 了解全国九年级学生身高的现状 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com