愉快的寒假南京出版社系列答案科目：初中数学 来源： 题型：
如图，已知抛物线y=ax2+bx+c（a≠0）的顶点坐标为Q(-2，-1)，且与y轴交于点C(0，3)，与x轴交于A，B两点（点A在点B的左侧），点P是该抛物线上一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作PD∥y轴，交直线AC于点D．
（1）求该抛物线的函数关系式．
（2）当△ADP是直角三角形时，求点P的坐标．
（3）在问题（2）的结论下，若点E在x轴上，点F在抛物线上，问是否存在以A，P，E，F为顶点的平行四边形？若存在，请直接写出点F的坐标；若不存在，请简单说明理由．
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
设a,b是任意两个不等实数，我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为{a,b},对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n时，有m≤y≤n,我们就称此函数是闭区间{m,n}上的“闭函数”.
（1）反比列函数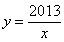
是闭区间{1,2013}上的“闭函数”吗？请判断并说明理由；
（2）若一次函数y=kx+b(k≠0)是闭区间{m,n}上的“闭函数”，求此函数的解析式：
查看答案和解析>>
科目：初中数学 来源： 题型：
19.如图，⊙O中，弦AB、CD相交于AB的中点E，连接AD并延长至点F，使DF=AD，
连接BC、BF．
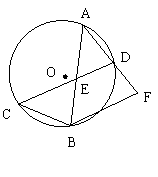（1）求证：△CBE∽△AFB；
（2）当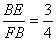
时，求
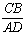的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
一个立方体展开后各面上分别标有数字1，2，3，4， 6，8，其表面展开图如图所示，抛掷这个立方体，则朝上一面的数字恰好等于朝下一面数字的2倍的概率是（ ）
A、
B、
C、
D、
查看答案和解析>>
科目：初中数学 来源： 题型：
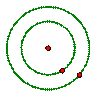
如图，在以O为圆心的两个同心圆中，大圆的直径AB交小圆于C、D两点，AC＝CD＝DB，分别以C、D为圆心，以CD为半径作圆．若AB＝6cm，则图中阴影部分的面积为 cm2．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，有2个同心圆，半径分别为R和r（单位：厘米）,且R>r>1，记两圆之间的圆环面积为P；若把R和r都增加1厘米，记两圆之间的圆环面积为Q，则：…………………………………………………( )
A： 0<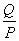
<1 B： 1<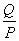<2 C： 2<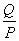<3 D： 3<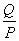<4
查看答案和解析>>
科目：初中数学 来源： 题型：
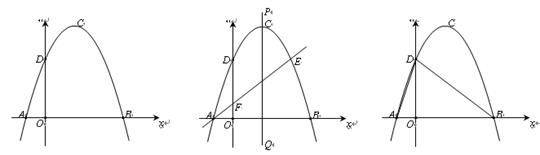
如图1，抛物线y=ax2＋bx＋c(a≠0)的顶点为（1,4），交x轴于A、B两点，交y轴于点D，其中B点的坐标为（3,0）.
（1）求抛物线的解析式.
（2）如图2，过点A的直线与抛物线交于点E，交y轴于点F，其中E点的横坐标为2，直线PQ为抛物线的对称轴.①说明点D与点E关于直线PQ对称.
②若点G为PQ上一动点，则x轴上是否存在一点H，使D、G、F、H四点围成的四边形周长最小？若存在，求出这个最小值及G、H的坐标；若不存在，请说明理由.
（3）如图3，抛物线上是否存在一点T，过点T作x的垂线，垂足为M，过点M作直线MN∥BD，交线段AD于点N，连接MD，使△DNM∽△BMD，若存在，求出点T的坐标；若不存在，说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的解是非负数，则m的取值范围是 ．