
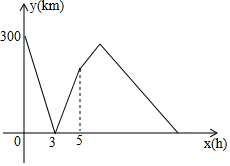
 甲,乙两车分别从A,B两地同时相向匀速行驶,乙车到达A地后未作停留,继续保持原速向远离B地的方向行驶,而甲车到达B地后修整了1个小时,然后调头并保持原速与乙车同向行驶,经过一段时间后两车同时到达C地.设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数图象如图所示,则A,C两地相距420千米.
甲,乙两车分别从A,B两地同时相向匀速行驶,乙车到达A地后未作停留,继续保持原速向远离B地的方向行驶,而甲车到达B地后修整了1个小时,然后调头并保持原速与乙车同向行驶,经过一段时间后两车同时到达C地.设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数图象如图所示,则A,C两地相距420千米. 分析 当x=0时,y=300,故此可得到AB两地的距离为300,3小时后两车相遇,从而可求得两车的速度之和,然后依据5小时后两车的距离变化,可知甲车到达B地用5小时,从而可乙车的速度,设甲、乙两车出发后经过t小时同时到达C地,根据甲乙两车的路程相差300千米,列方程可求得t的值,根据乙的路程得到B、C之间的距离,最后可得结论.
解答 解:由图象可得:当x=0时,y=300,
∴AB=300千米.
∴甲车的速度=300÷5=60千米/小时,
又∵300÷3=100千米/小时,
∴乙车的速度=100-60=40千米/小时,
设甲、乙两车出发后经过t小时同时到达C地,
依题意可得:60(t-1)-40t=300,
解得t=18,
∴B,C两地的距离=40×18=720千米,
则A,C两地相距:720-300=420千米,
故答案为:420.
点评 本题以行程问题为背景,主要考查了一次函数的应用,解决问题的关键是根据函数图象理解题意,求得两车的速度,并根据两车行驶路程的数量关系列出方程.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:解答题
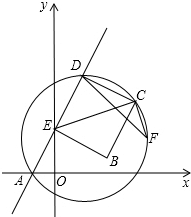 如图,直线y=2x+2与x轴,y轴分别交于A,E两点,D是第一象限内直线y=2x+2上运动的一个动点,以ED为边作正方形EDCB,连结CE,作EC⊥CF与过A,D,C三点的圆交于点F,连结DF.
如图,直线y=2x+2与x轴,y轴分别交于A,E两点,D是第一象限内直线y=2x+2上运动的一个动点,以ED为边作正方形EDCB,连结CE,作EC⊥CF与过A,D,C三点的圆交于点F,连结DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 快、慢两车分别从相距480km的甲,乙两地同时出发,匀速行驶,相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图象,则当两车第一次相遇时,快车距离甲地的路程是320千米.
快、慢两车分别从相距480km的甲,乙两地同时出发,匀速行驶,相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图象,则当两车第一次相遇时,快车距离甲地的路程是320千米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com