
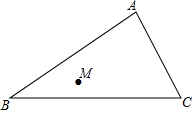
 已知△ABC及点M,试画出△A1B1C1和△A2B2C2,使△A1B1C1和△ABC关于点M成中心对称,使△A2B2C2和△ABC关于AC所在直线成轴对称.
已知△ABC及点M,试画出△A1B1C1和△A2B2C2,使△A1B1C1和△ABC关于点M成中心对称,使△A2B2C2和△ABC关于AC所在直线成轴对称. 科目:初中数学 来源: 题型:解答题
 如图所示,二次函数y=-x2+2x+3的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-x2+2x+3的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2016无锡“五一”车展期间,某公司对参观车展的且有购车意向的消费者进行了随机问卷调查,共发放900份调查问卷,并收回有效问卷750份.工作人员对有效调查问卷作了统计,其中,将消费者年收入的情况整理后,制成表格如下:
2016无锡“五一”车展期间,某公司对参观车展的且有购车意向的消费者进行了随机问卷调查,共发放900份调查问卷,并收回有效问卷750份.工作人员对有效调查问卷作了统计,其中,将消费者年收入的情况整理后,制成表格如下:| 年收入(万元) | 4.8 | 6 | 7.2 | 9 | 10 |
| 被调查的消费者人数(人) | 150 | 338 | 160 | 60 | 42 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com