
| A. | 300元 | B. | 310元 | C. | 320元 | D. | 330元 |
分析 设大人门票为x,小孩门票为y,根据题目给出的等量关系建立方程组,然后解出x、y的值,再代入计算即可.
解答 解:设大人门票为x,小孩门票为y,
由题意,得:$\left\{\begin{array}{l}{3x+4y=400}\\{4x+2y=400}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=80}\\{y=40}\end{array}\right.$,
则3x+2y=320.
即王斌家计划去3个大人和2个小孩,需要320元的门票.
故选:C.
点评 本题考查了二元一次方程组的应用,解答本题的关键是仔细审题,将实际问题转化为方程思想求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
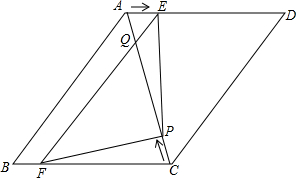 如图,在?ABCD中,AB=6cm,AD=AC=5cm,点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF,若运动时间为t(s)(0<t<2.5).解答下列问题:
如图,在?ABCD中,AB=6cm,AD=AC=5cm,点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF,若运动时间为t(s)(0<t<2.5).解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=500\\;}\\{5%x+4%y=4.5%}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=500\\;}\\{5%x+4%y=500×4.5%}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=500}\\{105%x+104%y=500+4.5%}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=500}\\{104%x+105%y=500×104.5%}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
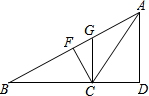 如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )
如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )| A. | △ABC中,AD是BC边上的高 | B. | △GBC中,CF是BG边上的高 | ||
| C. | △ABC中,GC是BC边上的高 | D. | △GBC中,GC是BC边上的高 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
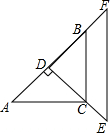 已知:有两块完全相同的含45°角的三角板,如图,将Rt△DEF的直角的顶点D放在Rt△ABC斜边AB的中点处,这时两块三角板重叠部分△DBC的面积是△ABC的面积的$\frac{1}{2}$.
已知:有两块完全相同的含45°角的三角板,如图,将Rt△DEF的直角的顶点D放在Rt△ABC斜边AB的中点处,这时两块三角板重叠部分△DBC的面积是△ABC的面积的$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com