
| A. | 13 | B. | 3或13 | C. | 3 | D. | 6 |
分析 本题没有给出图形,在画图时,应考虑到A、B、C三点之间的位置关系的多种可能,再根据题意画出的图形进行解答.
解答  解:设AB的中点与AC的中点分别是点M、N.
解:设AB的中点与AC的中点分别是点M、N.
如图1,MN=$\frac{1}{2}$AC-$\frac{1}{2}$AB=$\frac{1}{2}$×16-$\frac{1}{2}$×10=,3,
如图2,MN=$\frac{1}{2}$AC+$\frac{1}{2}$AB=$\frac{1}{2}$×16+$\frac{1}{2}$×10=13;
综上所述,AB的中点与AC的中点之间的距离是 3或13.
故选B.
点评 本题考查了两点间的距离.在未画图类问题中,正确画图很重要.本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2,-1 | B. | -2,1 | C. | -2,-1 | D. | 2,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
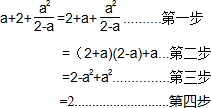
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-x-2=(x-1)(x+2) | B. | -a2+a-$\frac{1}{4}$=$-\frac{1}{4}(2a-1)^{2}$ | ||
| C. | a(x-y)-b(y-x)=(x-y)(a-b) | D. | x2-4+2x=(x+2)(x-2)+2x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
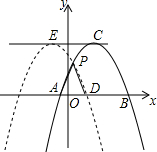 如图,抛物线y=-$\frac{4}{9}$(x-2)2+4交x轴于点A、B(点A在点B的左侧),其顶点为C,将抛物线沿x轴向左平移m(m>0)个单位,点B、C平移后的对应点为D、E,且两抛物线在x轴的上方交于点P,连接PA、PD.
如图,抛物线y=-$\frac{4}{9}$(x-2)2+4交x轴于点A、B(点A在点B的左侧),其顶点为C,将抛物线沿x轴向左平移m(m>0)个单位,点B、C平移后的对应点为D、E,且两抛物线在x轴的上方交于点P,连接PA、PD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com