
【题目】若二次函数![]() 图象的顶点在一次函数
图象的顶点在一次函数![]() 的图象上,则称
的图象上,则称![]() 为
为![]() 的伴随函数,如:
的伴随函数,如:![]() 是
是![]() 的伴随函数.
的伴随函数.
(1)若![]() 是
是![]() 的伴随函数,求直线
的伴随函数,求直线![]() 与两坐标轴围成的三角形的面积;
与两坐标轴围成的三角形的面积;
(2)若函数![]() 的伴随函数
的伴随函数![]() 与
与![]() 轴两个交点间的距离为4,求
轴两个交点间的距离为4,求![]() ,
,![]() 的值.
的值.
【答案】(1)8;(2)![]() ,
,![]() .
.
【解析】
(1)先求出二次函数的顶点,再把顶点代入一次函数求出p,再求出一次函数与坐标轴的交点坐标,再利用三角形的面积公式求解;
(2)先根据函数![]() 与
与![]() 轴两个交点间的距离为4,求出n,再求出二次函数的顶点,将顶点代入一次函数即可求解.
轴两个交点间的距离为4,求出n,再求出二次函数的顶点,将顶点代入一次函数即可求解.
解:(1)![]() ,
,
![]() 其顶点坐标为
其顶点坐标为![]() ,
,
![]() 是
是![]() 的伴随函数,
的伴随函数,
![]() 在一次函数
在一次函数![]() 的图象上,
的图象上,
![]() .
.
![]() ,
,
![]() 一次函数为:
一次函数为:![]() ,
,
![]() 一次函数与坐标轴的交点分别为
一次函数与坐标轴的交点分别为![]() ,
,![]() ,
,
![]() 直线
直线![]() 与两坐标轴围成的三角形的两直角边长度都为
与两坐标轴围成的三角形的两直角边长度都为![]() ,
,
![]() 直线
直线![]() 与两坐标轴围成的三角形的面积为:
与两坐标轴围成的三角形的面积为:![]() .
.
(2)设函数![]() 与
与![]() 轴两个交点的横坐标分别为
轴两个交点的横坐标分别为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
∵函数![]() 与
与![]() 轴两个交点间的距离为4,
轴两个交点间的距离为4,
![]() ,
,
解得,![]() ,
,
![]() 函数
函数![]() 为:
为:![]() ,
,
![]() 其顶点坐标为
其顶点坐标为![]() ,
,
![]() 是
是![]() 的伴随函数,
的伴随函数,
![]() ,
,
![]() .
.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 为正方形.点
为正方形.点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,一次函数
,一次函数![]() 的图象经过点
的图象经过点![]() 和点
和点![]() .
.
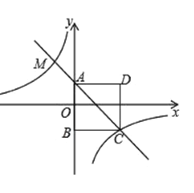
(1)求反比例函数与一次函数的解析式;
(2)写出![]() 的解集;
的解集;
(3)点![]() 是反比例函数图象上的一点,若
是反比例函数图象上的一点,若![]() 的面积恰好等于正方形
的面积恰好等于正方形![]() 的面积,求
的面积,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,一辆小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?______;(填“是”或“否”)请简述你的理由_______.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在同一直角坐标系中,二次函数的图象与两坐标轴分别交于点![]() 、点
、点![]() 和点
和点![]() ,一次函数的图象与抛物线交于
,一次函数的图象与抛物线交于![]() ,
,![]() 两点
两点
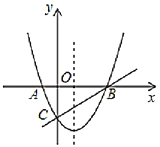
(1)求二次函数的表达式;
(2)当![]() 取什么值时,一次函数的函数值大于二次函数的函数值?
取什么值时,一次函数的函数值大于二次函数的函数值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,且点
两点,且点![]() 的横坐标是
的横坐标是![]() 点
点![]() 的横坐标是
的横坐标是![]() 则以下结论:
则以下结论:
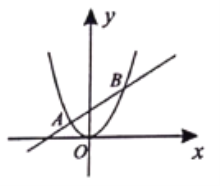
①![]() 时,直线
时,直线![]() 与抛物线
与抛物线![]() 的函数值都随着
的函数值都随着![]() 的增大而增大;②AB的长度可以等于5;③
的增大而增大;②AB的长度可以等于5;③![]() 有可能成为等边三角形;④当
有可能成为等边三角形;④当![]() 时,
时,![]() 时,其中正确的结论是( )
时,其中正确的结论是( )
A.①②B.①③C.①④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形![]() 中,
中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() (或它们的延长线)于点
(或它们的延长线)于点![]() .
.
当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),易证
时(如图1),易证![]() .
.
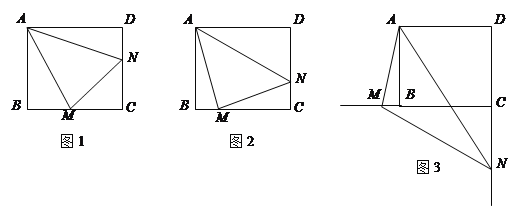
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图2),线段
时(如图2),线段![]() 和
和![]() 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.
(2)当![]() 绕点
绕点![]() 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段![]() 和
和![]() 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com