
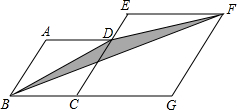
 如图,菱形ABCD和菱形ECGF的边长分别为2和4,∠A=120°,则图中阴影部分的面积是( )
如图,菱形ABCD和菱形ECGF的边长分别为2和4,∠A=120°,则图中阴影部分的面积是( )| A. | $\sqrt{3}$ | B. | $\frac{9}{4}$$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
分析 设BF交CE于点H,根据菱形的对边平行,利用相似三角形对应边成比例列式求出CH,然后求出DH,根据菱形邻角互补求出∠ABC=60°,再求出点B到CD的距离以及点G到CE的距离;然后根据阴影部分的面积=S△BDH+S△FDH,根据三角形的面积公式列式进行计算即可得解.
解答 解:如图,设BF交CE于点H,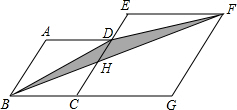
∵菱形ECGF的边CE∥GF,
∴△BCH∽△BGF,
∴CH:FG=BC:BG,
即CH:4=2:6,
解得CH=$\frac{4}{3}$,
所以,DH=CD-CH=2-$\frac{4}{3}$,
∵∠A=120°,
∴∠ECG=∠ABC=180°-120°=60°,
∴点B到CD的距离为2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
点G到CE的距离为4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴阴影部分的面积=S△BDH+S△FDH,
=$\frac{1}{2}$×$\frac{2}{3}×\sqrt{3}$+$\frac{1}{2}$×$\frac{2}{3}×2\sqrt{3}$=$\sqrt{3}$
故选A.
点评 本题考查了菱形的对边平行,邻角互补的性质,相似三角形对应边成比例的性质,求出DH的长度,把阴影部分的面积分成两个三角形的面积进行求解是解题的关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
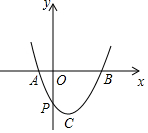 如图,已知二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点P,顶点为C(1,-2).
如图,已知二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点P,顶点为C(1,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
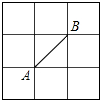 如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为轴对称图形,则点C的个数是( )
如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为轴对称图形,则点C的个数是( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
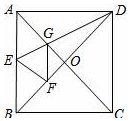 如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②$\frac{AD}{AE}$=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4$\sqrt{2}$,其中正确的结论个数为( )
如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②$\frac{AD}{AE}$=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4$\sqrt{2}$,其中正确的结论个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
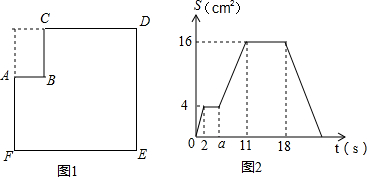
| A. | ①③④ | B. | ①②③ | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com