

���� ��1���Ƚⷽ�̣����ݵ�B�������ص�д��B��-4��3�����ٸ����۵������ʵó���F�����ꣻ
��2������������������ۣ���0��t��1ʱ���ص��������S�����ı���B��GEE���������������������1��t��4ʱ���ص��������S��������OGB��C������������ֱ����Ҳ�������ò���t=4ʱ��S=0��
��3�����ڣ���ͼ�ܢݢޣ���M����ֱ��MG��ֱ��MN�Ľ��㣬�����ʽ�����з�������⼴�ɣ�
���  �⣺��1����ͼ�٣�m2+m-12=0��
�⣺��1����ͼ�٣�m2+m-12=0��
��m-3����m+4��=0��
m1=3��m2=-4��
��B��-4��3����
��F��-1��3����
�ʴ�Ϊ����-4��3������-1��3����
��2����E����O�غ�ʱ��EO=EE��=4-3=1����ʱt=1����ͼ�ڣ�
��0��t��1ʱ����B��C��E�����ı���OABE�ص��������ı���B��GEE�䣬
��ƽ�Ƶã�BB��=EE�䣬BE��BE�䣬
��BB���EE�䣬
���ı���B��BEE����ƽ���ı��Σ�
��BC=EC=3����BCE=90�㣬
���CBE=45�㣬
���EBB��=��CBE=45�㣬
���BGB���ǵ���ֱ�������Σ�
��S=S?BEE��B��-S��BGB��=EE��•BC-$\frac{1}{2}$��BB���B��G=3t-$\frac{1}{2}{t}^{2}$=-$\frac{1}{2}{t}^{2}+3t$��
��1��t��4ʱ����ͼ�ۣ�
OC��=4-t��
��OE��=C��E��-OC��=3-��4-t��=t-1��
��OG��B��C�䣬
��$\frac{OG}{B��C��}$=$\frac{OE��}{C��E��}$��
��$\frac{OG}{3}=\frac{t-1}{3}$��
��OG=t-1��
��S=S��B��C��E��-S��GOE��=$\frac{9}{2}$-$\frac{1}{2}$��t-1��2=-$\frac{1}{2}$t2+t+4��
��t=4ʱ����C��O�غϣ���ʱS=0��
����������S��ƽ�ƾ���t֮��ĺ�����ϵʽΪ��
S=$\left\{\begin{array}{l}{-\frac{1}{2}{t}^{2}+3t��0��t��1��}\\{-\frac{1}{2}{t}^{2}+t+4��1��t��4��}\end{array}\right.$��
��3�����ڣ���ͼ�ܣ���N��y��������ʱ��
��MG�Ľ���ʽΪ��y=kx+b��
��C��-4��0����G��-1��1.5������ã�$\left\{\begin{array}{l}{-k+b=1.5}\\{-4k+b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=0.5}\\{b=2}\end{array}\right.$��
��MG��y=0.5x+2��
��H��0��2����
���ı���MNBG��ƽ���ı��Σ�
��BN��MG��
����BN�Ľ���ʽΪ��y=0.5x+n��
��B��-4��3������ã�n=5��
��BN��y=0.5x+5��
��N��0��5����
ͬ����BG��y=-0.5x+1��
��MN��BG��
��MN��y=-0.5x+5��
��$\left\{\begin{array}{l}{y=-0.5x+5}\\{y=0.5x+2}\end{array}\right.$ ���$\left\{\begin{array}{l}{x=3}\\{y=3.5}\end{array}\right.$��
��M��3��3.5����
��ͼ�ݣ���N��y�Ḻ����ʱ��
CG��y=0.5x+2��
����M��a��0.5a+2����
BG��y=-0.5x+1������MN��y=-0.5x+b��N��0��b����
��3-��0.5a+2��=1.5-b��
-0.5a+b=0.5�٣�
��M��a��0.5a+2������MN��0.5a+2=-0.5a+b��
a-b=-2�ڣ�
�ɢ٢ڵã�a=-3��b=-1��
��M��-3��0.5����
��ͼ�ޣ���BGΪ�Խ���ʱ��G��-1��$\frac{3}{2}$����
��EG=$\frac{3}{2}$��
��M��MP��BC��P����G��GQ��y����Q��
�á�BMP�ա�NGQ��
��MP=GQ=1��
��CE��MP��
���GCE=��CMP��
��tan��GCE=tan��CMP=$\frac{EG}{CE}=\frac{CP}{PM}$=$\frac{\frac{3}{2}}{3}$=$\frac{1}{2}$��
��CP=$\frac{1}{2}$��
��M��-5��-$\frac{1}{2}$����
�������������������ĵ�M������Ϊ��3��3.5������-3��0.5������-5��-$\frac{1}{2}$����
���� �������ı��ε��ۺ��⣬�ۺϿ�������Ρ�ƽ���ı��Ρ�����ֱ���������۵������ʣ����������һ�κ������ϣ�ͬʱ�������������ε�����ͽ�һԪ���η��̣�֪ʶ��϶ࣻ���������ν�Ϻͷ������۵�˼�룬ʹ������Խ����ͬʱ��Ҫע�Ȿ���е�t��ƽ�Ƶľ��룬����ʱ��t��


 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
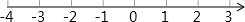 �ⲻ��ʽ�飺$\left\{\begin{array}{l}{4x��x-9}\\{\frac{1+3x}{2}��2x}\end{array}\right.$�����ѽ⼯�������ϱ�ʾ������
�ⲻ��ʽ�飺$\left\{\begin{array}{l}{4x��x-9}\\{\frac{1+3x}{2}��2x}\end{array}\right.$�����ѽ⼯�������ϱ�ʾ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �����в���ʽ��ʽ�飬������⼯�������ϱ�ʾ������
�����в���ʽ��ʽ�飬������⼯�������ϱ�ʾ�������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com