
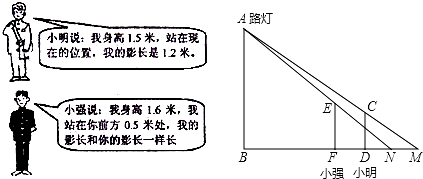
分析 (1)根据路灯与站着的人平行即可得到相似三角形;
(2)根据两人的影长一样长,结合图形可以得知MN=FD=0.5米,然后利用相似三角形对应边成比例的性质,根据小强与小明两种情况列出两个比例式,两式联立求解即可得到路灯的高度.
解答 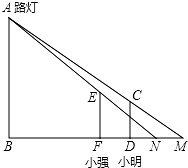 解:(1)△ABN~△EFN△ABM~△CDM;
解:(1)△ABN~△EFN△ABM~△CDM;
(2)根据题意,MN=FD=0.5米,
∵△ABM∽△CDM,
∴$\frac{CD}{AB}$=$\frac{DM}{BM}$,即$\frac{1.5}{AB}$=$\frac{1.2}{MB}$-----①,
∵△ABN∽△EFN,
∴$\frac{EF}{AB}$=$\frac{FN}{BN}$,即$\frac{1.6}{AB}$=$\frac{1.2}{BM-0.5}$-----②,
①②两式联立解得AB=10.
故路灯的高度10米.
点评 本题主要考查了相似三角形的应用,列出比例式是解题的关键,准确找出MN的长度是解本题的突破口,也是难点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
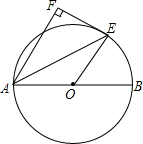 如图,AB是⊙O的直径,AE是弦,EF是圆O的切线,E是切点,AF⊥EF,垂足是F,AE平分∠FAB吗?为什么?探索:你能探究出线段AE与AF、AB之间的关系吗?
如图,AB是⊙O的直径,AE是弦,EF是圆O的切线,E是切点,AF⊥EF,垂足是F,AE平分∠FAB吗?为什么?探索:你能探究出线段AE与AF、AB之间的关系吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com