
【题目】已知抛物线c1的顶点为A(﹣1,4),与y轴的交点为D(0,3).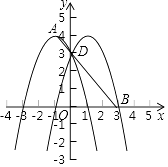
(1)求c1的解析式;
(2)若直线l1:y=x+m与c1仅有唯一的交点,求m的值;
(3)若抛物线c1关于y轴对称的抛物线记作c2 , 平行于x轴的直线记作l2:y=n.试结合图形回答:当n为何值时,l2与c1和c2共有:①两个交点;②三个交点;③四个交点;
(4)若c2与x轴正半轴交点记作B,试在x轴上求点P,使△PAB为等腰三角形.
【答案】
(1)
解:∵抛物线c1的顶点为A(﹣1,4),
∴设抛物线c1的解析式为y=a(x+1)2+4,
把D(0,3)代入y=a(x+1)2+4得3=a+4,
∴a=﹣1,
∴抛物线c1的解析式为:y=﹣(x+1)2+4,即y=﹣x2﹣2x+3
(2)
解:解 ![]() 得x2+3x+m﹣3=0,
得x2+3x+m﹣3=0,
∵直线l1:y=x+m与c1仅有唯一的交点,
∴△=9﹣4m+12=0,
∴m= ![]() ;
;
(3)
解:∵抛物线c1关于y轴对称的抛物线记作c2,
∴抛物线c2的顶点坐标为(1,4),与y轴的交点为(0,3),
∴抛物线c2的解析式为:y=﹣x2+2x+3,
∴①当直线l2过抛物线c1的顶点(﹣1,4)和抛物线记作c2的顶点(1,4)时,即n=4时,l2与c1和c2共有两个交点;
②当直线l2过D(0,3)时,即n=3时,l2与c1和c2共有三个交点;
③当3<n<4或n>3时,l2与c1和c2共有四个交点
(4)
解:如图,∵若c2与x轴正半轴交于B,
∴B(3,0),
∴OB=3,
∴AB= ![]() =4
=4 ![]() ,
,
①当AP=AB=4 ![]() 时,PB=8,
时,PB=8,
∴P1(﹣5,0),
②当AB=BP=4 ![]() 时,
时,
P2(3﹣4 ![]() ,0)或P3(3+4
,0)或P3(3+4 ![]() ,0),
,0),
③当AP=PB时,点P在AB的垂直平分线上,
∴PA=PB=4,
∴P4(﹣1,0),
综上所述,点P的坐标为(﹣5,0)或(3﹣4 ![]() ,0)或(3+4
,0)或(3+4 ![]() ,0)或(﹣1,0)时,△PAB为等腰三角形.
,0)或(﹣1,0)时,△PAB为等腰三角形.

【解析】(1)设抛物线c1的解析式为y=a(x+1)2+4,把D(0,3)代入y=a(x+1)2+4即可得到结论;(2)解方程组得到x2+3x+m﹣3=0,由于直线l1:y=x+m与c1仅有唯一的交点,于是得到△=9﹣4m+12=0,即可得到结论;(3)根据轴对称的性质得到抛物线c2的解析式为:y=﹣x2+2x+3,根据图象即可刚刚结论;(4)求得B(3,0),得到OB=3,根据勾股定理得到AB= ![]() =4
=4 ![]() ,①当AP=AB,②当AB=BP=4
,①当AP=AB,②当AB=BP=4 ![]() 时,③当AP=PB时,点P在AB的垂直平分线上,于是得到结论.
时,③当AP=PB时,点P在AB的垂直平分线上,于是得到结论.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】有一根40cm的金属棒,欲将其截成x根7cm的小段和y根9cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )
A.x=1,y=3
B.x=4,y=1
C.x=3,y=2
D.x=2,y=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=2,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=1,若△ABE与以D、M、N为顶点的三角形相似,则DM= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD、BC分别交于点E、F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.
(1)求证:①△DOK≌△BOG;②AB+AK=BG;
(2)若KD=KG,BC=4﹣ ![]() .
.
①求KD的长度;
②如图2,点P是线段KD上的动点(不与点D、K重合),PM∥DG交KG于点M,PN∥KG交DG于点N,设PD=m,当S△PMN= ![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( ) 
A.3≤OM≤5
B.4≤OM≤5
C.3<OM<5
D.4<OM<5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求 ![]() 的值;
的值;
(3)在(2)的条件下,若 ![]() =k(k为大于
=k(k为大于 ![]() 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A. (a2+2b2)﹣2(﹣a2+b2)=3a2+b2
B.![]() ﹣a﹣1=
﹣a﹣1= ![]()
C. (﹣a)3m÷am=(﹣1)ma2m
D. 6x2﹣5x﹣1=(2x﹣1)(3x﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( ) ①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG:S△HBG=tan∠DAG ⑤线段DH的最小值是2 ![]() ﹣2.
﹣2.
A.2
B.3
C.4
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com