

·ÖĪö £Ø1£©øł¾ŻBĘ·ÖÖÓŠ120¶Ö£¬Õ¼30%¼“æÉĒóµĆµ÷²éµÄÕāČżÖÖĄóÖ¦µÄ×ܶ֏ż£»
£Ø2£©øł¾Żø÷Ę·ÖÖÖŹĮæÖ®ŗĶµČÓŚ400æɵĆCĘ·ÖÖÖŹĮ棬ŌŁÓĆAĖłÕ¼±ČĄż³ĖŅŌ360¶ČæɵƓš°ø£»
£Ø3£©×ÜŹżĮæ300³ĖŅŌCĘ·ÖÖĄóÖ¦µÄ¶ÖŹżĖłÕ¼µÄ°Ł·Ö±Č¼“æÉĒó½ā£®
½ā“š ½ā£ŗ£Ø1£©120”Ā30%=400£Ø¶Ö£©£®
“š£ŗøĆŹŠ³”6ŌĀÉĻ°ėŌĀ¹²ĻśŹŪÕāČżÖÖĄóÖ¦400¶Ö£»
£Ø2£©CĘ·ÖÖµÄĮćŹŪĮæĪŖ400-40-120=240£Ø¶Ö£©£¬
Ķ¼2ÖŠAĖłŌŚÉČŠĪµÄŌ²ŠÄ½ĒµÄ¶ČŹżĪŖ$\frac{40}{400}$”Į360”ć=36”ć£¬
²¹Č«Ķ¼ĻóČēĻĀ£ŗ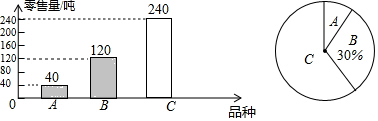
£Ø3£©300”Į$\frac{240}{400}$=180£ØĒ§æĖ£©£®
“š£ŗøĆÉĢ³”Ó¦¹ŗ½ųCĘ·ÖÖĄóÖ¦180Ē§æĖ±Č½ĻŗĻĄķ£®
µćĘĄ ±¾Ģāæ¼²éµÄŹĒĢõŠĪĶ³¼ĘĶ¼ŗĶÉČŠĪĶ³¼ĘĶ¼µÄ×ŪŗĻŌĖÓĆ£¬¶Į¶®Ķ³¼ĘĶ¼£¬“Ó²»Ķ¬µÄĶ³¼ĘĶ¼ÖŠµĆµ½±ŲŅŖµÄŠÅĻ¢ŹĒ½ā¾öĪŹĢāµÄ¹Ų¼ü£®ĢõŠĪĶ³¼ĘĶ¼ÄÜĒ峞µŲ±ķŹ¾³öĆæøöĻīÄæµÄŹż¾Ż£»ÉČŠĪĶ³¼ĘĶ¼Ö±½Ó·“Ó³²æ·ÖÕ¼×ÜĢåµÄ°Ł·Ö±Č“󊔣®


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
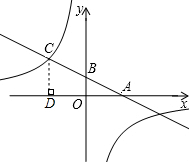 ČēĶ¼£¬ŅŃÖŖŅ»“ĪŗÆŹży=ax+b£Øa£¬bĪŖ³£Źż£¬a”Ł0£©µÄĶ¼ĻóÓėxÖį£¬yÖį·Ö±š½»ÓŚµćA£¬B£¬ĒŅÓė·“±ČĄżŗÆŹży=$\frac{k}{x}$£ØkĪŖ³£Źż£¬k”Ł0£©µÄĶ¼ĻóŌŚµŚ¶žĻóĻŽÄŚ½»ÓŚµćC£¬×÷CD”ĶxÖįÓŚD£¬ČōOA=OD=$\frac{3}{4}$OB=3£®
ČēĶ¼£¬ŅŃÖŖŅ»“ĪŗÆŹży=ax+b£Øa£¬bĪŖ³£Źż£¬a”Ł0£©µÄĶ¼ĻóÓėxÖį£¬yÖį·Ö±š½»ÓŚµćA£¬B£¬ĒŅÓė·“±ČĄżŗÆŹży=$\frac{k}{x}$£ØkĪŖ³£Źż£¬k”Ł0£©µÄĶ¼ĻóŌŚµŚ¶žĻóĻŽÄŚ½»ÓŚµćC£¬×÷CD”ĶxÖįÓŚD£¬ČōOA=OD=$\frac{3}{4}$OB=3£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com