【题目】已知二次函数y=ax2+bx+c的图象上部分点的横坐标x与纵坐标y的对应值如下表：
那么关于它的图象，下列判断正确的是（ ）
A. 开口向上 B. 与x轴的另一个交点是（3，0）
C. 与y轴交于负半轴 D. 在直线x=1的左侧部分是下降的
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB＝AC，点D、E、F分别在AB、BC、AC边 且BE＝CF，AD+EC＝AB．
（1）求证：△DEF是等腰三角形；
（2）当∠A＝40°时，求∠DEF的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（
分）如图，在
中， 
， 
， 
，点
在边
上运动， 
平分
交边
于点
， 
垂足为
， 
垂足为
．
（
）当
时，求证： 
．
（
）探究： 
为何值时， 
与
相似？
（
）直接写出： 
__________时，四边形
与
的面积相等．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知正方形 ABCO，边长是 4，点 D(a，0)，以 AD 为边在AD 的右侧作等腰 Rt△ADE，∠ADE＝90°，连接 OE，则 OE 的最小值为__________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，直线
，点
为平面内一点，连接
与
.
（1）如图1，点在直线
、
之间，若
，
，求
的度数.
（2）如图2，点在直线、之间，
与
的角平分线相交于点
，写出
与之间的数量关系，并说明理由.
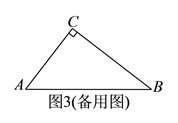
（3）如图3，点在直线下方，与的角平分线相交于点，直接写出与的数量关系.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】己知一次函数
，
（1）无论 k为何值，函数图像必过定点，求该点的坐标；
（2）如图 1，当 k=-
时，该直线交 x 轴，y 轴于 A，B 两点，直线 l2:y=x+1 交 AB 于点 P，点 Q 是 l2 上一点，若 SABQ 6 ，求 Q 点的坐标；
（3）如图 2，在第 2 问的条件下，已知 D 点在该直线上，横坐标为 1，C 点在 x 轴负半轴， ABC=45 ，动点 M 的坐标为（a，a），求 CM+MD 的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读以下材料：
对数的创始人是苏格兰数学家纳皮尔（J. Nplcr，1550-1617年），纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evlcr，1707-1783年）才发现指数与对数之间的联系.
对数的定义：一般地，若
，那么
叫做以
为底
的对数，记作：
.比如指数式
可以转化为
，对数式
可以转化为
.
我们根据对数的定义可得到对数的一个性质：
；理由如下：
设
，
，则
，
∴
，由对数的定义得
又∵
∴
解决以下问题：
（1）将指数
转化为对数式______；
（2）证明
（3）拓展运用：计算
______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某天，一蔬菜经营户用90元钱从蔬菜批发市场批了西红柿和豆角共40kg到菜市场去卖，西红柿和豆角这天的批发价与零售价如下表所示：
品名 | 西红柿 | 豆角 |
批发价（单位：元/kg） | 2.5 | 1.5 |
零售价（单位：元/kg） | 3.5 | 2.8 |
问：（1）西红柿和豆角的重量各是多少？（列二元一次方程组求解）
（2）他当天卖完这些西红柿和豆角能赚多少钱？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某餐厅中，一张桌子可坐6人，有如图所示的两种摆放方式：
（1）当有n张桌子时，两种摆放方式各能坐多少人？
（2）一天中午餐厅要接待98位顾客共同就餐，但餐厅只有25张这样的餐桌.若你是这个餐厅的经理，你打算选择哪种方式来摆放餐桌？为什么？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
