
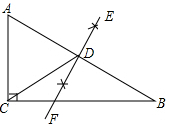
 如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )
如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )| A. | 13 | B. | 17 | C. | 18 | D. | 25 |
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:初中数学 来源: 题型:选择题
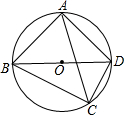 已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )
已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )| A. | AC=BC+CD | B. | $\sqrt{2}$AC=BC+CD | C. | $\sqrt{3}$AC=BC+CD | D. | 2AC=BC+CD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
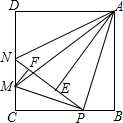 如图,在正方形ABCD中,AB=4,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处,在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.
如图,在正方形ABCD中,AB=4,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处,在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,点P是BC边上一点(不与B、C重合),连接PA,将线段PA绕点P顺时针旋转90°得到线段PE,交边DC于F,连接AE,CE.
如图,在正方形ABCD中,点P是BC边上一点(不与B、C重合),连接PA,将线段PA绕点P顺时针旋转90°得到线段PE,交边DC于F,连接AE,CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com