
分析 (1)根据已知等式猜想即可得到结果;
(2)原式各项利用猜想的结论计算即可得到结果;
(3)原式利用拆项法变形,计算即可得到结果.
解答 解:(1)猜想:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)①原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2013}$-$\frac{1}{2014}$=1-$\frac{1}{2014}$=$\frac{2013}{2014}$;
②原式=$\frac{1}{100}$-$\frac{1}{101}$+$\frac{1}{101}$-$\frac{1}{102}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{1}{100}$-$\frac{1}{n+1}$=$\frac{n-99}{100(n+1)}$;
(3)原式=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{2012}$-$\frac{1}{2014}$)=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{2014}$)=$\frac{503}{4028}$.
故答案为:(1)$\frac{1}{n}$-$\frac{1}{n+1}$;(2)①$\frac{2013}{2014}$;②$\frac{n-99}{100(n+1)}$
点评 此题考查了有理数的混合运算,弄清题中的规律是解本题的关键.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
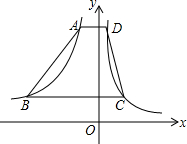 如图,在横跨第一、二象限的梯形ABCD中,AD∥BC∥x轴,AD=1,BC=4,它的高为4,四个顶点都在反比例函数的图象上,则关于A,B两点坐标说法错误的是( )
如图,在横跨第一、二象限的梯形ABCD中,AD∥BC∥x轴,AD=1,BC=4,它的高为4,四个顶点都在反比例函数的图象上,则关于A,B两点坐标说法错误的是( )| A. | A点的横坐标是-$\frac{3}{5}$,B点的横坐标是-3 | |
| B. | A点的横坐标是-$\frac{3}{5}$,B点的纵坐标是$\frac{4}{3}$ | |
| C. | A点的纵坐标是$\frac{16}{3}$,B点的横坐标是-3 | |
| D. | A点的纵坐标是$\frac{16}{3}$,B点的纵坐标是$\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com