
 ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌЁїAOBЮЊЕШБпШ§НЧаЮЃЌЕуAЕФзјБъЪЧЃЈ4$\sqrt{3}$ЃЌ0ЃЉЃЌЕуBдкЕквЛЯѓЯоЃЌACЪЧЁЯOABЕФЦНЗжЯпЃЌВЂЧвгыyжсНЛгкЕуEЃЌЕуMЮЊжБЯпACЩЯвЛИіЖЏЕуЃЌАбЁїAOMШЦЕуAЫГЪБеыа§зЊЃЌЪЙБпAOгыБпBжиКЯЃЌЕУЕНЁїABDЃЎМйЩшЗДБШР§КЏЪ§y=$\frac{k}{x}$ЃЈxЃО0ЃЉЭМЯѓОЙ§ЕуB
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌЁїAOBЮЊЕШБпШ§НЧаЮЃЌЕуAЕФзјБъЪЧЃЈ4$\sqrt{3}$ЃЌ0ЃЉЃЌЕуBдкЕквЛЯѓЯоЃЌACЪЧЁЯOABЕФЦНЗжЯпЃЌВЂЧвгыyжсНЛгкЕуEЃЌЕуMЮЊжБЯпACЩЯвЛИіЖЏЕуЃЌАбЁїAOMШЦЕуAЫГЪБеыа§зЊЃЌЪЙБпAOгыБпBжиКЯЃЌЕУЕНЁїABDЃЎМйЩшЗДБШР§КЏЪ§y=$\frac{k}{x}$ЃЈxЃО0ЃЉЭМЯѓОЙ§ЕуBЗжЮі ЃЈ1ЃЉЕБMгыЕуEжиКЯЪБЃЌЗДБШР§КЏЪ§y=$\frac{k}{x}$ЕФЭМЯѓВЛОЙ§ADЕФжаЕуЃЎРэгЩЃКЩшADЕФжаЕуЮЊЕуFЃЌзїBHЁЭOAЃЌгЩЁїAOBЮЊЕШБпШ§НЧаЮЃЌЕуAЕФзјБъЪЧЃЈ4$\sqrt{3}$ЃЌ0ЃЉЃЌПЩЧѓГіOA=OB=4$\sqrt{3}$ЃЌOH=HA=$\frac{1}{2}$OA=2$\sqrt{3}$ЃЌШЛКѓдкRtЁїBOHжаЃЌгЩЙДЙЩЖЈРэПЩЧѓBHЕФжЕЃЌНјЖјШЗЖЈBЕуЕФзјБъЃЌгЩЗДБШР§КЏЪ§y=$\frac{k}{x}$ЃЈxЃО0ЃЉЭМЯѓОЙ§ЕуBЃЌДгЖјШЗЖЈЗДБШР§КЏЪ§ЕФЙиЯЕЪНЃКy=$\frac{12\sqrt{3}}{x}$ЃЌШЛКѓгЩACЪЧЁЯOABЕФЦНЗжЯпЃЌПЩЕУЁЯOAE=ЁЯBAE=30ЁуЃЌдкRtЁїAOEжаЃЌгЩ30ЁуНЧЫљЖдЕФжБНЧБпЕШгкаББпЕФвЛАыЃЌПЩЕУOE=$\frac{1}{2}$AEЃЌгЩЙДЙЩЖЈРэЕУЃКOA2+OE2=AE2ЃЌПЩЧѓЃКOE=4ЃЌНјЖјПЩЕУAE=8ЃЌгЩЁїAOMШЦЕуAЫГЪБеыа§зЊЃЌЪЙБпAOгыБпABжиКЯЃЌЕУЕНЁїABDЃЌИљОна§зЊЕФаджЪЃЌПЩЕУAD=AE=8ЃЌЁЯDAB=ЁЯMAO=30ЁуЃЌНјЖјПЩЕУЁЯAOD=90ЁуЃЌгЩЕуFЪЧADЕФжаЕуЃЌПЩЕУЕуFЕФзјБъЮЊЃКЃЈ4$\sqrt{3}$ЃЌ4ЃЉЃЌШЛКѓНЋFЕуЕФзјБъДњШыЙиЯЕЪНЃЌбщжЄЕуFВЛдкЗДБШР§КЏЪ§y=$\frac{12\sqrt{3}}{x}$ЕФЭМЯѓЩЯЃЌДгЖјЕУЕНЃКЕБMгыЕуEжиКЯЪБЃЌЗДБШР§КЏЪ§y=$\frac{k}{x}$ЕФЭМЯѓВЛОЙ§ADЕФжаЕуЃЛ
ЃЈ2ЃЉДцдкЕуMЃЌЪЙЗДБШР§КЏЪ§y=$\frac{k}{x}$ЕФЭМЯѓБиОЙ§ADЕФжаЕуЃЎгЩЃЈ1ЃЉжЊЃКOE=4ЃЌНјЖјШЗЖЈEЃЈ0ЃЌ4ЃЉЃЌШЛКѓЩшжБЯпACЕФЙиЯЕЪНЮЊЃКy=kx+bЃЌНЋAЃЈ4$\sqrt{3}$ЃЌ0ЃЉЃЌEЃЈ0ЃЌ4ЃЉДњШыЩЯЪіЙиЯЕЪНЃЌДгЖјПЩЕУжБЯпACЕФЙиЯЕЪНЮЊЃКy=-$\frac{\sqrt{3}}{3}$x+4ЃЌгЩЕуMдкжБЯпACЩЯЃЌПЩЩшMЕФзјБъЮЊЃКЃЈaЃЌ-$\frac{\sqrt{3}}{3}$a+4ЃЉЃЌНјЖјПЩЕУMP=-$\frac{\sqrt{3}}{3}$a+4ЃЌШЛКѓгЩ30ЁуНЧЫљЖдЕФжБНЧБпЕШгкаББпЕФвЛАыЃЌПЩЕУAM=2MP=-$\frac{2\sqrt{3}}{3}a$+8ЃЌгЩЁїAOMШЦЕуAЫГЪБеыа§зЊЃЌЪЙБпAOгыБпABжиКЯЃЌЕУЕНЁїABDЃЌИљОна§зЊЕФаджЪЃЌПЩЕУAD=AM=-$\frac{2\sqrt{3}}{3}$a+8ЃЌЁЯDAB=ЁЯMAO=30ЁуЃЌНјЖјПЩЕУЁЯAOD=90ЁуЃЌДгЖјШЗЖЈADЕФжаЕуЕФзјБъЃЌгЩЗДБШР§КЏЪ§y=$\frac{k}{x}$ЕФЭМЯѓБиОЙ§ADЕФжаЕуЃЌНЋADЕФжаЕуЃЌДњШыy=$\frac{12\sqrt{3}}{x}$ЃЌДгЖјШЗЖЈMЕФзјБъЃЎ
НтД№ НтЃКЃЈ1ЃЉЕБMгыЕуEжиКЯЪБЃЌЗДБШР§КЏЪ§y=$\frac{k}{x}$ЕФЭМЯѓВЛОЙ§ADЕФжаЕуЃЎ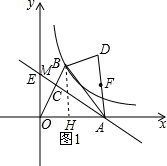
РэгЩЃКЩшADЕФжаЕуЮЊЕуFЃЌзїBHЁЭOAЃЌ
ЁпЁїAOBЮЊЕШБпШ§НЧаЮЃЌЕуAЕФзјБъЪЧЃЈ4$\sqrt{3}$ЃЌ0ЃЉЃЌ
ЁрOA=OB=4$\sqrt{3}$ЃЌOH=HA=$\frac{1}{2}$OA=2$\sqrt{3}$ЃЌЁЯOAB=60ЁуЃЌ
дкRtЁїBOHжаЃЌгЩЙДЙЩЖЈРэЕУЃКBH=$\sqrt{O{B}^{2}-O{H}^{2}}$=6ЃЌ
ЁрBЕуЕФзјБъЮЊЃКЃЈ2$\sqrt{3}$ЃЌ6ЃЉЃЌ
ЁрЗДБШР§КЏЪ§y=$\frac{k}{x}$ЃЈxЃО0ЃЉЭМЯѓОЙ§ЕуBЃЌ
Ёрk=xy=12$\sqrt{3}$ЃЌ
ЁрЗДБШР§КЏЪ§ЕФЙиЯЕЪНЃКy=$\frac{12\sqrt{3}}{x}$ЃЌ
ЁпACЪЧЁЯOABЕФЦНЗжЯпЃЌ
ЁрЁЯOAE=ЁЯBAE=30ЁуЃЌ
дкRtЁїAOEжаЃЌ
ЁпЁЯOAE=30ЁуЃЌ
ЁрOE=$\frac{1}{2}$AEЃЌ
гЩЙДЙЩЖЈРэЕУЃКOA2+OE2=AE2ЃЌ
МДЃЈ4$\sqrt{3}$ЃЉ2+OE2=ЃЈ2OEЃЉ2ЃЌ
НтЕУЃКOE=4ЃЌ
ЁрAE=8ЃЌ
ЁпЁїAOMШЦЕуAЫГЪБеыа§зЊЃЌЪЙБпAOгыБпABжиКЯЃЌЕУЕНЁїABDЃЎ
ЁрAD=AE=8ЃЌЁЯDAB=ЁЯMAO=30ЁуЃЌ
ЁрЁЯAOD=ЁЯOAB+ЁЯDAB=90ЁуЃЌ
ЁпЕуFЪЧADЕФжаЕуЃЌ
ЁрЕуFЕФзјБъЮЊЃКЃЈ4$\sqrt{3}$ЃЌ4ЃЉЃЌ
ЕБx=4$\sqrt{3}$ЪБЃЌy=$\frac{12\sqrt{3}}{4\sqrt{3}}$=3Ёй4ЃЌ
ЁрЕуFВЛдкЗДБШР§КЏЪ§y=$\frac{12\sqrt{3}}{x}$ЕФЭМЯѓЩЯЃЌ
МДЕБMгыЕуEжиКЯЪБЃЌЗДБШР§КЏЪ§y=$\frac{k}{x}$ЕФЭМЯѓВЛОЙ§ADЕФжаЕуЃЎ
ЃЈ2ЃЉДцдкЕуMЃЌЪЙЗДБШР§КЏЪ§y=$\frac{k}{x}$ЕФЭМЯѓБиОЙ§ADЕФжаЕуЃЎ
гЩЃЈ1ЃЉжЊЃКOE=4ЃЌ
ЁрEЃЈ0ЃЌ4ЃЉЃЌ
ЩшжБЯпACЕФЙиЯЕЪНЮЊЃКy=kx+bЃЌ
НЋAЃЈ4$\sqrt{3}$ЃЌ0ЃЉЃЌEЃЈ0ЃЌ4ЃЉДњШыЩЯЪіЙиЯЕЪНЕУЃК
$\left\{\begin{array}{l}{b=4}\\{4\sqrt{3}k+b=0}\end{array}\right.$ЃЌ
НтЕУЃК$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=4}\end{array}\right.$ЃЌ
ЁржБЯпACЕФЙиЯЕЪНЮЊЃКy=-$\frac{\sqrt{3}}{3}$x+4ЃЌ
ЁпЕуMдкжБЯпACЩЯЃЌ
ЁрЩшMЕФзјБъЮЊЃКЃЈaЃЌ-$\frac{\sqrt{3}}{3}$a+4ЃЉЃЌ
ЁрMP=-$\frac{\sqrt{3}}{3}$a+4ЃЌ
ЁпЁЯMAO=30ЁуЃЌ
ЁрAM=2MP=-$\frac{2\sqrt{3}}{3}a$+8ЃЌ
ЁпЁїAOMШЦЕуAЫГЪБеыа§зЊЃЌЪЙБпAOгыБпABжиКЯЃЌЕУЕНЁїABDЃЎ
ЁрAD=AM=-$\frac{2\sqrt{3}}{3}$a+8ЃЌЁЯDAB=ЁЯMAO=30ЁуЃЌ
ЁрЁЯAOD=ЁЯOAB+ЁЯDAB=90ЁуЃЌ
ЁрADЕФжаЕуЕФзјБъЮЊЃКЃЈ4$\sqrt{3}$ЃЌ-$\frac{\sqrt{3}}{3}$a+4ЃЉЃЌ
ЁпЗДБШР§КЏЪ§y=$\frac{k}{x}$ЕФЭМЯѓБиОЙ§ADЕФжаЕуЃЌ
ЁрНЋADЕФжаЕуЕФзјБъЃЈ4$\sqrt{3}$ЃЌ-$\frac{\sqrt{3}}{3}$a+4ЃЉЃЌДњШыy=$\frac{12\sqrt{3}}{x}$ЕУЃК
-$\frac{\sqrt{3}}{3}$a+4=$\frac{12\sqrt{3}}{4\sqrt{3}}$ЃЌ
НтЕУЃКa=-$\sqrt{3}$ЃЌ
ЁрMЃЈ-$\sqrt{3}$ЃЌ5ЃЉЃЎ
МДДцдкЕуMЃЈ-$\sqrt{3}$ЃЌ5ЃЉЃЌЪЙЗДБШР§КЏЪ§y=$\frac{12\sqrt{3}}{x}$ЕФЭМЯѓБиОЙ§ADЕФжаЕуЃЎ
ЕуЦР ДЫЬтЪЧЗДБШР§КЏЪ§ЕФзлКЯЬтЃЌжївЊПМВщСЫЃКгУД§ЖЈЯЕЪ§ЗЈЧѓЙиЯЕЪНЁЂЙДЙЩЖЈРэЁЂдкЦНУцжБНЧзјБъЯЕФкШЗЖЈЕуЕФзјБъЕШжЊЪЖЃЌНтЬтЕФЙиМќЪЧЃКУїШЗЭМаЮЕФа§зЊВЛИФБфЭМаЮЕФДѓаЁгыаЮзДЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
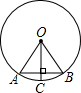 ШчЭМЃЌдкЁбOжаЃЌЯвABЕШгкЁбOЕФАыОЖЃЌOCЁЭABНЛЁбOгкЕуCЃЌдђЁЯAOCЕШгкЃЈЁЁЁЁЃЉ
ШчЭМЃЌдкЁбOжаЃЌЯвABЕШгкЁбOЕФАыОЖЃЌOCЁЭABНЛЁбOгкЕуCЃЌдђЁЯAOCЕШгкЃЈЁЁЁЁЃЉ| AЃЎ | 80Ёу | BЃЎ | 50Ёу | CЃЎ | 40Ёу | DЃЎ | 30Ёу |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 1 | BЃЎ | -27 | CЃЎ | 1Лђ-27 | DЃЎ | ЮоЗЈШЗЖЈ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
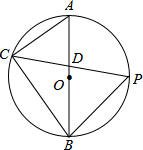 ШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЕуPЪЧ$\widehat{AB}$ЕФжаЕуЃЎ
ШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЕуPЪЧ$\widehat{AB}$ЕФжаЕуЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ШчЭМЃЌГЄЗНаЮABCDЕФУцЛ§ЮЊ60ЦНЗНРхУзЃЌAE=EBЃЌBF=FCЃЌCG=GDЃЌHЮЊADБпЩЯШЮвтвЛЕуЃЌвѕгАВПЗжУцЛ§КЭГЄЗНаЮABCDУцЛ§ЕФБШЪЧ1ЃК2ЃЎ
ШчЭМЃЌГЄЗНаЮABCDЕФУцЛ§ЮЊ60ЦНЗНРхУзЃЌAE=EBЃЌBF=FCЃЌCG=GDЃЌHЮЊADБпЩЯШЮвтвЛЕуЃЌвѕгАВПЗжУцЛ§КЭГЄЗНаЮABCDУцЛ§ЕФБШЪЧ1ЃК2ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌвбжЊжБЯпlЃК$y=\sqrt{3}x+3$гыxжсЁЂyжсНЛгкAЁЂBСНЕуЃЌНЋжБЯпlЯђЯТЦНвЦmИіЕЅЮЛГЄЖШКѓЕУжБЯпl1ЃЌжБЯпl1гыxжсЁЂyжсЗжБ№НЛгкCЁЂDСНЕуЃЌНЋЁїCODШЦЕуOбиФцЪБеыЗНЯђа§зЊ60ЁуКѓЕУЕНЁїCЁфOЁфDЁфЃЎШєЁїAOBЁеЁїCODЃК
ШчЭМЃЌвбжЊжБЯпlЃК$y=\sqrt{3}x+3$гыxжсЁЂyжсНЛгкAЁЂBСНЕуЃЌНЋжБЯпlЯђЯТЦНвЦmИіЕЅЮЛГЄЖШКѓЕУжБЯпl1ЃЌжБЯпl1гыxжсЁЂyжсЗжБ№НЛгкCЁЂDСНЕуЃЌНЋЁїCODШЦЕуOбиФцЪБеыЗНЯђа§зЊ60ЁуКѓЕУЕНЁїCЁфOЁфDЁфЃЎШєЁїAOBЁеЁїCODЃКВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 дкаЁПзГЩЯёЮЪЬтжаЃЌИљОнШчЭМЫљЪОЃЌШєOЕНABЕФОрРыЪЧ18cmЃЌOЕНCDЕФОрРыЪЧ6cmЃЌдђЯёCDЕФГЄЪЧЮяABГЄЕФЃЈЁЁЁЁЃЉ
дкаЁПзГЩЯёЮЪЬтжаЃЌИљОнШчЭМЫљЪОЃЌШєOЕНABЕФОрРыЪЧ18cmЃЌOЕНCDЕФОрРыЪЧ6cmЃЌдђЯёCDЕФГЄЪЧЮяABГЄЕФЃЈЁЁЁЁЃЉ| AЃЎ | 3БЖ | BЃЎ | $\frac{1}{2}$ | ||
| CЃЎ | $\frac{1}{3}$ | DЃЎ | ВЛжЊABЕФГЄЖШЃЌЮоЗЈХаЖЯ |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com