
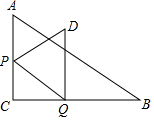
 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=6,点P、Q分别在AC、BC边上,PQ∥AB.将线段PQ绕点P按逆时针方向旋转60°,得到线段PD,连接DQ.设PC=x.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=6,点P、Q分别在AC、BC边上,PQ∥AB.将线段PQ绕点P按逆时针方向旋转60°,得到线段PD,连接DQ.设PC=x.分析 (1)根据有一个角是60°的等腰三角形是等边三角形得出:△PQD是等边三角形;
(2)点Q在∠CAB的平分线上,即AQ平分∠CAB,则∠CAQ=∠BAQ=30°,根据30°角的正切列式可求出x的值;
(3)先求出当点D在AB上时,如图2,x=2,分两种情况进行讨论:
①当0≤x≤2时,如图3,重叠部分是等边三角形PDQ,即T=6x;
②当2<x<6时,如图4,重叠部分是四边形EPQF,分别计算四边的长,相加可得T与x之间的函数关系式.
解答 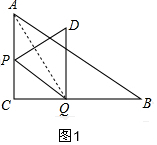 解:(1)△PQD是等边三角形,理由是:
解:(1)△PQD是等边三角形,理由是:
由旋转得:PQ=PD,∠QPD=60°,
∴△PQD是等边三角形;
(2)连接AQ,
当AQ平分∠CAB时,∠CAQ=∠BAQ=30°,
在Rt△ACQ中,tan30°=$\frac{CQ}{AC}$,
CQ=AC•tan30°=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$,
∵PQ∥AB,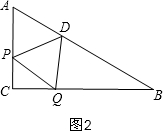
∴∠PQC=∠B=30°,
在Rt△PCQ中,tan30°=$\frac{PC}{CQ}$,
PC=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2,
即x=2,
则当x=2时,点Q在∠CAB的平分线上;
(3)当点D在AB上时,如图2,
在Rt△PCQ中,∠CQP=30°,PC=x,
∴PQ=2x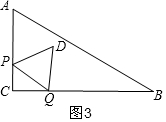 ,
,
∵∠CQP=30°,∠PQD=60°,
∴∠CQD=90°,
∴BD=2DQ=4x,
由勾股定理得:CQ=$\sqrt{3}$x,BQ=$\sqrt{(4x)^{2}-(2x)^{2}}$=2$\sqrt{3}$x,
∴BC=3$\sqrt{3}$x,
在Rt△ABC中,tan30°=$\frac{AC}{BC}$,
BC=$\frac{6}{\frac{\sqrt{3}}{3}}$=6$\sqrt{3}$,
∴6$\sqrt{3}$=3$\sqrt{3}$x,
x=2,
此时T=3PQ=6x=12;
分两种情况:
①当0≤x≤2时,如图3,重叠部分是等边三角形PDQ,
此时,T=△PQD的周长=3PQ=6x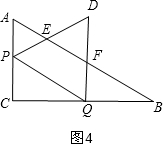 ,
,
②当2<x<6时,如图4,重叠部分是四边形EPQF,
∵PC=x,
∴AP=6-x,
∵∠CPQ=∠DPQ=60°,
∴∠APE=60°,
∵∠A=60°,
∴∠AEP=60°,
∴△AEP是等边三角形,
∴AP=AE=PE=6-x,
∵EF∥PQ,
∴∠DEF=∠DPQ=60°,∠DFE=∠DQP=60°,
∵∠D=60°,
∴△DEF是等边三角形,
∴DE=EF=DF=2x-(6-x)=3x-6,
∴QF=6-x,
∴T=PQ+FQ+EP+EF=2x+6-x+6-x+3x-6=3x+6,
综上所述,T与x之间的函数关系式为:T=$\left\{\begin{array}{l}{6x(0≤x≤2)}\\{3x+6(2<x<6)}\end{array}\right.$.
点评 本题是几何变换综合题,难度适中,考查的是旋转变换的性质、角平分线的性质、等边三角形的性质,本题的特殊角较多,利用了三角函数的特殊值列式求边长,同时采用了分类讨论的思想,并与图形相结合,先确定特殊位置时对应的x的值,才能确定其各种情况的取值范围.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
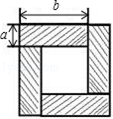 如图是用4个全等的长方形拼成的一个“回形”正方形,将图中阴影部分面积用2种方法表示可得一个等式,这个等式为(a+b)2-(b-a)2=4ab.
如图是用4个全等的长方形拼成的一个“回形”正方形,将图中阴影部分面积用2种方法表示可得一个等式,这个等式为(a+b)2-(b-a)2=4ab.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 里程 | 收费(元) |
| 起步费3千米以下(含3千米) | 3 |
| 3千米以上,每增加1千米 | 1.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com