
分析 (1)估算出$\sqrt{5}$和$\sqrt{37}$的大致范围,然后可求得a、b的值,然后再求代数式的值即可.
(2)先求得x的值,然后再表示出y-$\sqrt{3}$的值,最后进行计算即可.
解答 解:(1)∵4<5<9,36<37<49,
∴2<$\sqrt{5}$<3,6<$\sqrt{37}$<7.
∴a=$\sqrt{5}$-2,b=6.
∴a+b-$\sqrt{5}$=$\sqrt{5}$-2+6-$\sqrt{5}$=4.
(2)∵1<$\sqrt{3}$<2,
∴9<8+$\sqrt{3}$<10,
∴x=9.
∵y=8+$\sqrt{3}$-x.
∴y-$\sqrt{3}$=8-x=-1.
∴原式=3×9-1=26.
点评 本题主要考查的是估算无理数的大小,求得y-$\sqrt{3}$的值的大小是解题的关键.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:填空题
 我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.
我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 15 | C. | 12或15 | D. | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6,3,1 | B. | 3,6,1 | C. | 2,1,3 | D. | 2,3,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
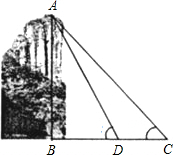 如图,为测得峰顶A到河面B的高度,当游船行至C处时测得峰顶A的仰角为45°,前进20米至D处时测得峰顶A的仰角为60°(此时C、D、B三点在同一直线上),求峰顶A到河面B的高度.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$=1.73)
如图,为测得峰顶A到河面B的高度,当游船行至C处时测得峰顶A的仰角为45°,前进20米至D处时测得峰顶A的仰角为60°(此时C、D、B三点在同一直线上),求峰顶A到河面B的高度.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$=1.73)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com