
【题目】如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥底面圆的圆心,圆锥的高为2![]() m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.
m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.
(1)求∠ABC的度数;
(2)若∠ACP=2∠ABC,求光源A距水平面的高度.

【答案】(1)∠ABC=30°;(2)4![]() m.
m.
【解析】(1),过点D作DF垂直BC于点F,则在Rt△DFB中,运用正切函数tan∠B=DFBF,即可以求出∠ABC的度数;
(2),结合已知条件∠ACP=2∠B以及三角形的外角性质,可求出∠BAC=30 °,进而依据等角对等边可得AC=BC=8,过点A作AH垂直BP于点H构造Rt△ACH,并在直角三角形中运用正弦函数可求出AH=ACSin∠ACP,至此本题可解.
(1)如图,过点D作DF⊥BC于点F.
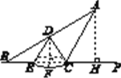
由题意,得DF=2![]() m,EF=2 m,BE=4 m.
m,EF=2 m,BE=4 m.
在Rt△DFB中,BF=BE+EF=4+2=6(m),
∴DB=![]() =
=![]() =4
=4![]() (m),
(m),
∴DF=![]() DB,
DB,
∴∠ABC=30°.
(2)如图,过点A作AH⊥BP,垂足为H.
∵∠ACP=2∠ABC=60°,
∴∠BAC=30°,
∴AC=BC=8 m.
在Rt△ACH中,AH=8sin60°=8×![]() =4
=4![]() (m),即光源A距水平面的高度为4
(m),即光源A距水平面的高度为4![]() m.
m.


科目:初中数学 来源: 题型:
【题目】为了丰富学生的课余生活,宣传我县的旅游景点,某校将举行“我为松桃旅游代言”的活动,现随机抽取了部分学生进行主题为“你想去的景点是 ”的问卷调查,要求学生只能去“![]() (正大苗王成),
(正大苗王成),![]() (寨英古镇),
(寨英古镇),![]() (盘石黔东草海),
(盘石黔东草海),![]() (乌罗潜龙洞)”四个景点选择一项,根据调查结果,绘制了如下两幅不完整的统计图.回答下列问题:
(乌罗潜龙洞)”四个景点选择一项,根据调查结果,绘制了如下两幅不完整的统计图.回答下列问题:

⑴本次共调查了多少名学生;
⑵请把条形统计图补充完整;
⑶该学校共有3000名学生,试估计该校最想去盘石黔东草海的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() .
.

(1)如图①,在平面直角坐标系中,以![]() 为顶点,
为顶点,![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() ,若
,若![]() ,求
,求![]() 点的坐标;
点的坐标;
(2)如图②,![]() 为
为![]() 轴负半轴上一个动点,以
轴负半轴上一个动点,以![]() 为顶点,
为顶点,![]() 为腰作等腰
为腰作等腰![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,当
点,当![]() 点沿
点沿![]() 轴负半轴向下运动时,试问
轴负半轴向下运动时,试问![]() 的值是否发生变化?若不变,求其值,若变化,请说明理由;
的值是否发生变化?若不变,求其值,若变化,请说明理由;
(3)如图③,已知点![]() 坐标为
坐标为![]() ,
,![]() 是
是![]() 轴负半轴上一点,以
轴负半轴上一点,以![]() 为直角边作等腰
为直角边作等腰![]() ,
,![]() 点在
点在![]() 轴上,
轴上,![]() ,设
,设![]() 、
、![]() ,当
,当![]() 点在
点在![]() 轴的负半轴上沿负方向运动时,
轴的负半轴上沿负方向运动时,![]() 的和是否发生变化?若不变,求其值;若变化,请说明理由.
的和是否发生变化?若不变,求其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
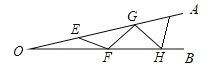
【题目】如图,![]() 是一钢架,且
是一钢架,且![]() ,为使钢架更加牢固,需在其内部添加-一些钢管
,为使钢架更加牢固,需在其内部添加-一些钢管![]() 、
、![]() 、
、![]() ,添加的钢管都与
,添加的钢管都与![]() 相等,则最多能添加这样的钢管( )
相等,则最多能添加这样的钢管( )
A.![]() 根B.
根B.![]() 根C.
根C.![]() 根D.无数根
根D.无数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义,如果一个四边形有一条对角线能将其分成一个等边三角形和一个直角三角形,那么这个四边形叫做等垂四边形,这条对角线叫做这个四边形的等垂对角线.
(1)已知![]() 是四边形
是四边形![]() 的等垂对角线,
的等垂对角线,![]() ,
,![]() 均为钝角,且
均为钝角,且![]() 比
比![]() 大
大![]() ,那么
,那么![]() ________.
________.
(2)如图,已知![]() 与
与![]() 关于直线
关于直线![]() 对称,
对称,![]() 、
、![]() 两点分别在
两点分别在![]() 、
、![]() 边上,
边上,![]() ,
,![]() ,
,![]() .求证:四边形
.求证:四边形![]() 是等垂四边形。
是等垂四边形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(a),将两块直角三角尺的直角顶点C叠放在一起.
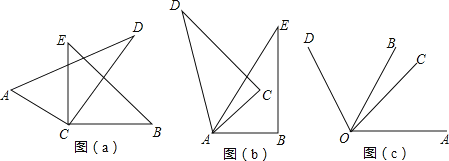
(1)若∠DCE=35°,∠ACB= ;若∠ACB=140°,则∠DCE= ;并猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(2)如图(b),若是两个同样的三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小有何关系,请说明理由;
(3)已知∠AOB=α,∠COD=β(都是锐角),如图(c),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的大小相等的关系(用含有α,β的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
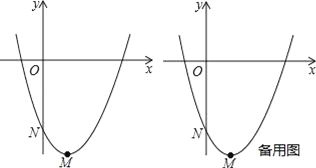
【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,BC边上有10个不同的点P1,P2,……,P10, 记![]() (i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
(i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
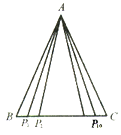
A. 4 B. 14 C. 40 D. 不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com