
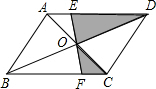
 如图,?ABCD的面积是8,对角线AC、DB交于点O,EF过点O分别交AD、BC于E、F,则阴影部分的面积是( )
如图,?ABCD的面积是8,对角线AC、DB交于点O,EF过点O分别交AD、BC于E、F,则阴影部分的面积是( )| A. | 4 | B. | 2 | C. | 6 | D. | 无法确定 |
分析 先根据平行四边形的性质得出OB=OD,∠FBO=∠EDO,再由全等三角形的判定得到△OFB≌△OED,从而将阴影部分的面积转化为规则的几何图形的面积进行计算.
解答 解:∵四边形ABCD是平行四边形,
∴OB=OD,∠FBO=∠EDO.
在△OFB与△OED中
$\left\{\begin{array}{l}{∠FBO=∠EDO}\\{OB=OD}\\{∠FOB=∠EOD}\end{array}\right.$,
∴△FBO≌△EDO,
∴S阴影部分=S△BOC=$\frac{1}{4}$S?ABCD=$\frac{1}{4}$×8=2.
故选B.
点评 本题主要考查了平行四边形的性质以及全等三角形的判定,并通过此题让学生明白求阴影部分的面积一般的思路是将不规则的阴影部分转化为规则的几何图形求解.


科目:初中数学 来源: 题型:选择题
| A. | y1≤y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象经过第二象限 | B. | 函数值y随x的增大而减小 | ||
| C. | 图象在x轴上的截距是1 | D. | 图象在y轴上的截距是-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
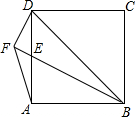 如图,四边形ABCD是正方形,点E是边AD上一点,DF⊥BE,交BE的延长线于点F,连接AF.若DF=1,AF=$\sqrt{2}$,则BD的长是$\sqrt{10}$.
如图,四边形ABCD是正方形,点E是边AD上一点,DF⊥BE,交BE的延长线于点F,连接AF.若DF=1,AF=$\sqrt{2}$,则BD的长是$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{16}$=±4 | B. | $\root{3}{27}$=-3 | C. | ±$\sqrt{16}$=4 | D. | $\sqrt{(-4)^{3}}$=-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com