
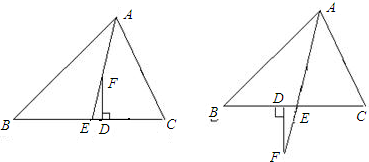
 ∠C-
∠C- ∠B,理由如下:
∠B,理由如下: ∠BAC,
∠BAC, ∠BAC+∠EFD=90°;①
∠BAC+∠EFD=90°;① ∠C+
∠C+ ∠B+
∠B+ ∠BAC=90°,②
∠BAC=90°,② ∠C-
∠C- ∠B.
∠B. ∠BAC,所以∠B+
∠BAC,所以∠B+ ∠BAC+∠EFD=90°,联立△ABC中,由三角形内角和定理得到的式子,即可推出∠EFD,∠B,∠C的关系.
∠BAC+∠EFD=90°,联立△ABC中,由三角形内角和定理得到的式子,即可推出∠EFD,∠B,∠C的关系.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com